Пусть функции z1(x,y) и z2(x,y) определены и непрерывны в ограниченной замкнутой области D и z1(x,y) £ z2(x,y). Область G={(x,y,z)|(x,y)ÎD, z1(x,y) £ z £ z2(x,y)} называется z –цилиндрической. Аналогично определяются х –цилиндрическая и y –цилиндрическая области. Область G называется простой, если ее можно разбить на конечное число как х –цилиндрических, так и y –цилиндрических и z ‑цилиндрических областей.
Теорема. Пусть функции P(x,y,z), Q(x,y,z), R(x,y,z), и их частные производные 
непрерывны в простой замкнутой области G, ограниченной кусочно-гладкой поверхностью Ф. Тогда справедлива формула
, (1)
где поверхностный интеграл берется на внешней стороне поверхности Ф, которая служит границей G.
Формула (1) называется формулой Остроградского-Гаусса.
Следствие. Если функции P, Q, R таковы, что 
, то интеграл в левой части равенства
(1) равен объему области G, т.е.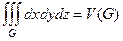 
, и из формулы (1) получается формула для вычисления объема области G с помощью интеграла по ее поверхности:
(2)
