Пусть в области G определено векторное поле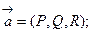 
L – замкнутый контур, лежащий в области G; Ф - произвольная поверхность, границей которой является контур L; Ф Ì G (говорят "поверхность Ф натянута на контур L "); 
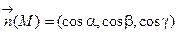–единичный вектор нормали на выбранной стороне поверхности Ф.
Поверхность Ф называется xyz – проектируемой, если она однозначно проектируется на каждую координатную плоскость прямоугольной системы координат Oxyz. Такую поверхность можно задать с помощью любого из уравнений: z=z(x,y), (x,y) Î G1; x=x(y,z), (y,z) Î G2; y=y(z,x), (z,x) Î G3.
Пусть Ф – гладкая xyz – проектируемая ориентированная поверхность, ограниченная кусочно-гладким контуром L и расположенная внутри области G, в которой функции P(x,y,z), Q(x,y,z), R(x,y,z) имеет непрерывные частные производные первого порядка. Тогда справедлива формула Стокса
где ориентация контура L согласована с ориентацией поверхности Ф. Левая часть формулы Стокса есть циркуляция векторного поля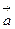 
вдоль контура L, а правая часть представляет собой поток через поверх
ность Ф векторного поля с координатами 
Эта формула названа по имени английского физика и математика Д. Стокса. Её формулу можно переписать также в следующем виде:
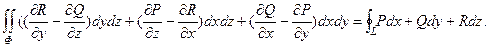
Формула Стокса остается верной для иной ориентированной поверхности Ф с кусочно-гладким краем L, которую можно разбить при помощи кусочно-гладких линий на конечное число гладких кусков, проецирующихся на все три плоскости координат. Ориентированная поверхность, которую можно разбить на конечное число и плоского треугольников, называется полиэдральной поверхностью и представляет собой пример простейшей поверхности, к которой применима формула Стокса.
