27. Вычислить циркуляцию плоского векторного поля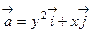 
вдоль кривой x= 3cos t, y= sin t с
обходом по часовой стрелке.
Решение. Данная кривая является эллипсом. Обход кривой совершается по часовой стрелке, поэтому t меняется от 2p до 0. Следовательно, циркуляция вычисляется следующим образом: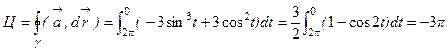 
. Ответ: –3p
28. Вычислить циркуляцию вектора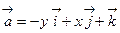 
вдоль окружности 
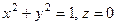в положительном направлении.
Решение. Параметрическое уравнение окружности: x =cos t, y =sin t, z =0, 0 £ t £ 2 p. Поскольку P = –y =
= ‑ sin t, Q=x= cos t, R= 1, dx= – sin tdt, dy= cos tdt, dz=0, то по определению циркуляции получаем:
.
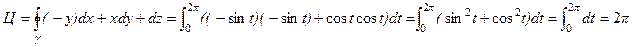Ответ: 2p
29. Найти циркуляцию векторного поля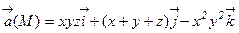 
вдоль контура квадрата
ABCDA, определяемого уравнениями: –x+y=a; x+y=a; x–y=a; x+y=–a; z= 0. См. рис. 2.
Решение. Имеем: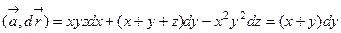 
, так как z= 0 и dz= 0. Разбиваем искомую циркуляцию на четыре линейных интеграла, причем в качестве параметра на каждой стороне квадрата выбираем координату y:
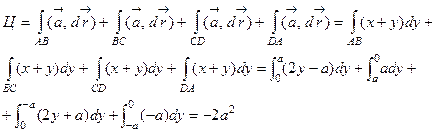
Ответ: –2а2.
