Векторное поле 
называют потенциальным в области (G), если существует такая скалярная функция (скалярное поле) 
, заданная в (G), что для всех точек этой области: 
. Функцию называют потенциалом поля 
.
В потенциальном поле линейный интеграл не зависит от формы пути и определятся только начальной и конечной точками пути, а именно
где М0 и М – начальная и конечная точка линии (L).
Верно и обратное: если линейный интеграл поля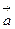 
(М) не зависит от пути, то поле 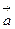(М) потенциально. Потенциал поля определяется с точностью до постоянного слагаемого. Это означает, что если 
один из потенциалов поля , то выражения 
при любом постоянном С также являются потенциалами поля. Задание величины потенциала в какой- либо точке М0 области (V) однозначно определяет потенциал любой точки М:
, (*)
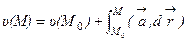где вместо 
использовано обозначение 
, поскольку интеграл не зависит от пути.
Если поле задано в декартовой координатной форме: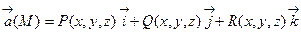 
, то для нахождения потенциала точки М(x,y,z) удобно взять линейный интеграл по ломанной М0М1М2М , звенья которой параллельны координатным осям.
Предполагается, конечно, что ломаная М0М1М2М не выходит за пределы области (G). При таком выборе пути интегрирования и при дополнительном условии 
выражение (*) принимает вид:
(*)
При использовании этой формулы следует иметь в виду, что в каждом из трех входящих в нее интегралов одной буквой обозначают и верхний предел, и переменную интегрирования, т.е.
Рис. 5.
Отметим, что потенциальность поля и равенство нулю циркуляции поля по искомому простому кусочно-гладкому замкнутому контуру являются эквивалентными свойствами.
Если поле потенциально в области (G), то в любой точке этой области 
. Это свойство потенциального поля является наиболее важным. Таким образом, потенциальное поле 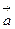(М) является безвихревым. Обратное, вообще говоря, неверно. Однако, если ограничиться поверхностно односвязными областями, то для таких областей понятие потенциального и безвихревого полей оказываются эквивалентными.
