Пряма, яка задана в умові цієї задачі, представляє собою лінію перетину двох площин 
та 
, рівняння яких записані у системі. Щоб скласти канонічне рівняння цієї прямої, необхідно знайти точку на прямій та її напрямний вектор (Рис.31.2).
Спочатку знайдемо точку на прямій. Для цього потрібно знайти будь-який розв’язок системи.
Розв’яжемо цю систему:
Додавши рівняння системи, отримаємо
, або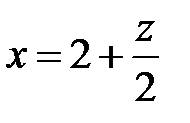 
.
Додавши перше рівняння системи, помножене на (-3), до другого, знайдемо
, тобто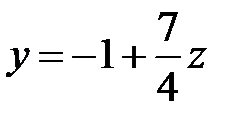 
.
Отже, система набуде вигляду:
.
Зафіксуємо вільну змінну: нехай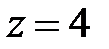 
, тоді 
. Отже, точка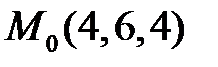 
лежить на заданій прямій.
Тепер знайдемо напрямний вектор прямої:
Тоді канонічне рівняння прямої має вигляд:
, або 
.
Задача 33.4. Знайти гострий кут між прямими 
та 
.
