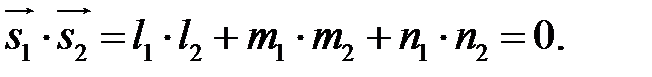Нехай є пряма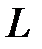 
, що у системі координат 
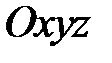задається рівнянням
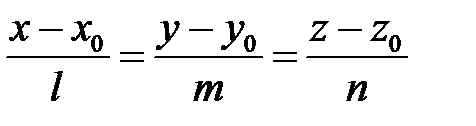
і точка 
. Через пряму і точку поза нею можна провести єдину площину. Проведемо таку площину через пряму та точку 
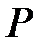(Рис.32.1). На площині проведемо 
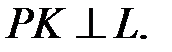Тоді довжина перпендикуляра 
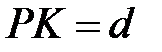і є відстань від точки до прямої.
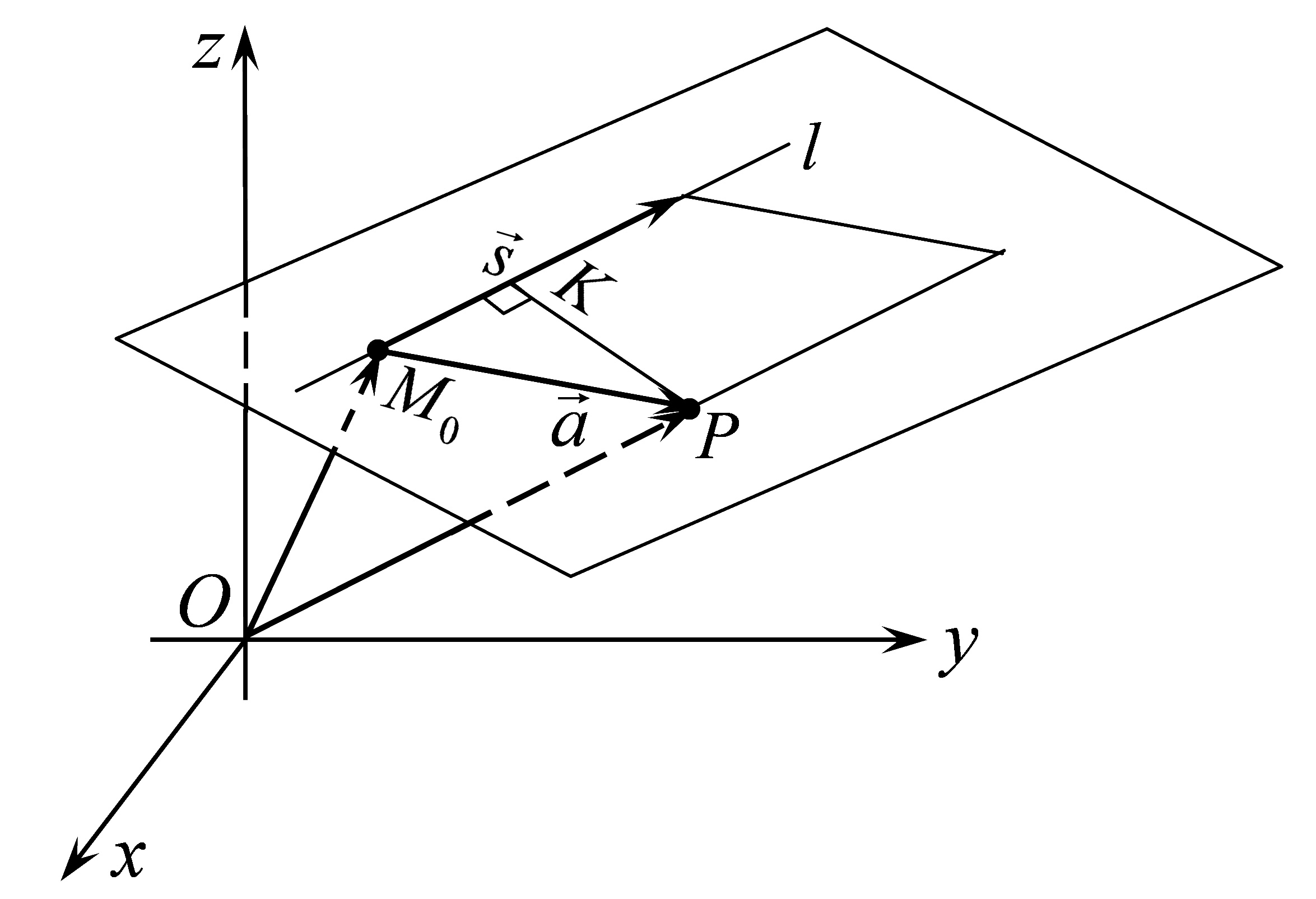
Рис.32.1
Для її знаходження на векторах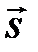 
і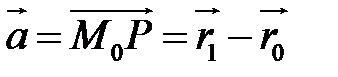 
будується паралелограм (Рис.32.1).
З одного боку його площа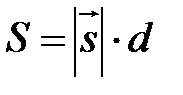 
, з іншого - 
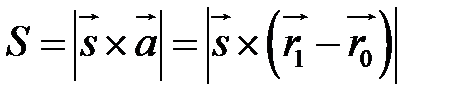. Отже
і
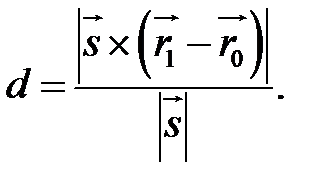
Розглянемо тепер дві прямі, які задані канонічними рівняннями
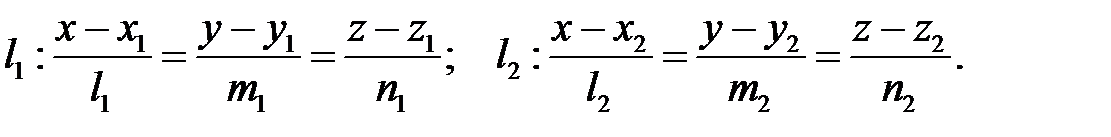
Для взаємного розміщення прямих у просторі можливі такі варіанти:
1) прямі паралельні або співпадають;
2) прямі перетинаються;
3) прямі не паралельні і не співпадають (мимобіжні).
Якщо прямі паралельні,то їх напрямні вектори 
і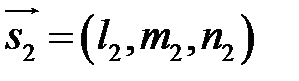 
колінеарні. Тому умовою паралельності прямих є умова колінеарності напрямних векторів:
Якщо прямі співпадають, то вектор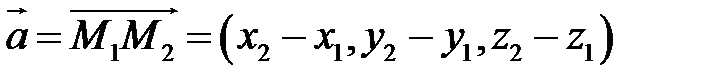 
теж колінеарний до векторів 
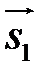і 
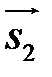. Тому умовою співпадання прямих є одночасне виконання умови і наступної рівності:
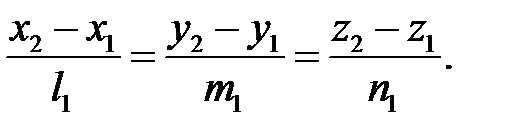
У випадку порушення умови прям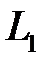і 
і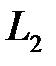 
або перетинаються, або є мимобіжними. Якщо прямі перетинаються, то вони розміщуються у одній площині, тоді вектори 
- компланарні. Умовою компланарності векторів є рівність нулю їх змішаного добутку:
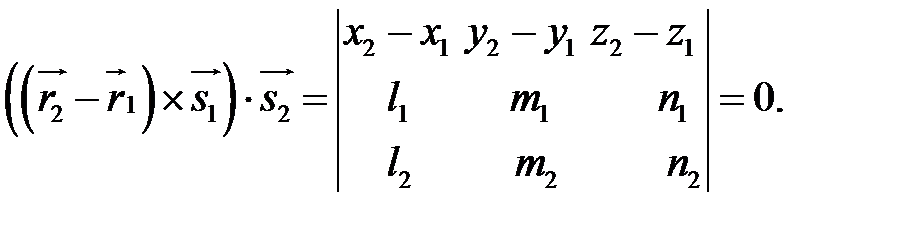
При порушенні умов і прям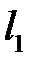і 
і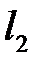 
мимобіжні.
Нехай тепер прям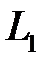і 
і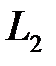 
перетинаються або мимобіжні. Тоді кут між їх напрямними векторами 
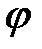співпадає з гострим кутом 
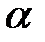або тупим 
кутом, що утворюють ці прямі (Рис.32.2)
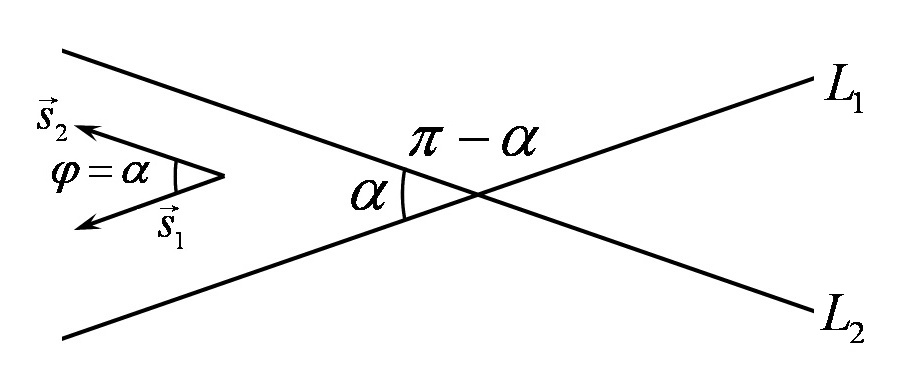
Рис.32.2
Кут між напрямними векторами знаходиться за формулою
Якщо результат за формулою додатний, то 
, а якщо від'ємний, то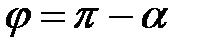 
. У випадку перпендикулярності прямих виконується рівність
