Нехай на осі 
площина відтинає відрізок довжини 
, тоді на двох інших осях відрізки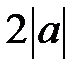 
.Використаємо рівняння площини у відрізках:
.
Точка 
належить площині, отже, її координати задовольняють рівняння:
.
З останього рівняння знаходимо, що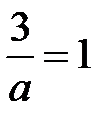 
, отже, 
.
Таким чином, рівняння площини має вигляд:
.
Задачі для самостійної роботи
1. Площина проходить через точку 
перпендикулярно вектору 
. Знайти відрізки, які вона відтинає на координатних осях.
2. Знайти рівняння площини, яка проходить через точку 
паралельно площині, що проходить через три точки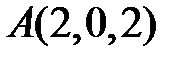 
, 
, 
.
3. Обчислити відстань від точки 
до площини 
.
4. При якому значенні 
площини 
та 
будуть перпендикулярні?
5. Знайти косинус кута між площинами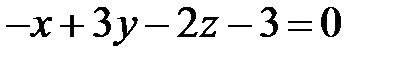 
та 
.
6. Скласти рівняння площини, що проходить через точку 
паралельно площині 
.
7. Скласти рівняння площини, яка проходить через вісь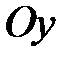 
та точку 
8. Скласти рівняння площини, яка проходить через точки 
, 
паралельно осі 
.
9. Записати рівняння площини, що проходить через точку 
і відтинає на координатних осях відрізки однакової довжини.
10. Довести, що площини 
та 
паралельні та знайти відстань між ними.
11. Записати рівняння площини, що проходить через точки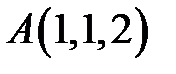 
та 
перпендикулярно до площини 
.
Питання для повторення
1) Лінія у просторі, її векторне та параметричне рівняння. Сферична поверхня.
2) Дослідження загального рівняння площини.
3) Кут між площинами, умови паралельності та перпендикулярності.
