Будь-яка пряма у просторі може бути задана за допомогою точки  ,через яку вона проходить, і ненульового вектора
,через яку вона проходить, і ненульового вектора 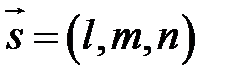 , до якого вона паралельна (Рис.31.1):
, до якого вона паралельна (Рис.31.1):

Рис.31.1
Нехай  - довільна точка прямої. Розглянемо вектори
- довільна точка прямої. Розглянемо вектори  ,
,  . Тоді вектор
. Тоді вектор  Для будь якої точки
Для будь якої точки  , що належить прямій, вектори
, що належить прямій, вектори  і
і  є колінеарними і за умов колінеарності виконується рівність:
є колінеарними і за умов колінеарності виконується рівність:

Рівняння називається канонічним рівнянням прямої у просторі. Вектор  , до якого пряма паралельна, називається її напрямним вектором.
, до якого пряма паралельна, називається її напрямним вектором.
З іншого боку, з колінеарності векторів 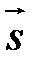 і
і 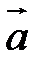 випливає, що існує число
випливає, що існує число  таке, що
таке, що  , або
, або


Рівняння називається векторним рівнянням прямої у просторі.
Якщо рівняння переписати покоординатно, то отримаємо рівності

Рівняння - це параметричне рівняння прямої у просторі.
Будь-яка пряма однозначно визначається своїми двома точками. Нехай точки  належать прямій. Візьмемо на цій прямій довільну точку
належать прямій. Візьмемо на цій прямій довільну точку 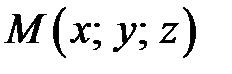 . Тоді вектори
. Тоді вектори  і
і  завжди знаходяться на одній прямій, а значить є колінеарними. З умови колінеарності векторів маємо
завжди знаходяться на одній прямій, а значить є колінеарними. З умови колінеарності векторів маємо

Таким чином, рівняння прямої, що проходить через дві задані точки має вигляд.
Пряма, як і будь яка інша лінія у просторі, може бути задана загальним рівнянням вигляду. У цьому випадку її необхідно розглядати як результат перетину двох непаралельних площин. При завданні площин загальними рівняннями загальне рівняння прямої, згідно (1.3) має набувати вигляду

Рівняння визначає у просторі пряму за умови, що нормальні вектори площин  не є колінеарними. Тоді один з визначників другого порядку, складених з координат цих векторів, відмінний від 0 і ранг матриці системи та її розширеної матриці дорівнює 2. Отже, ця система завжди сумісна і має нескінченну кількість розв’язків. Нехай
не є колінеарними. Тоді один з визначників другого порядку, складених з координат цих векторів, відмінний від 0 і ранг матриці системи та її розширеної матриці дорівнює 2. Отже, ця система завжди сумісна і має нескінченну кількість розв’язків. Нехай  - один з них. Тоді точка
- один з них. Тоді точка  належить прямій, що визначається. Оскільки вектори
належить прямій, що визначається. Оскільки вектори  і
і  є перпендикулярними до прямої, що утворена перетином площин, то вектор, що дорівнює їх векторному добутку (Рис.31.2), знаходиться так:
є перпендикулярними до прямої, що утворена перетином площин, то вектор, що дорівнює їх векторному добутку (Рис.31.2), знаходиться так:
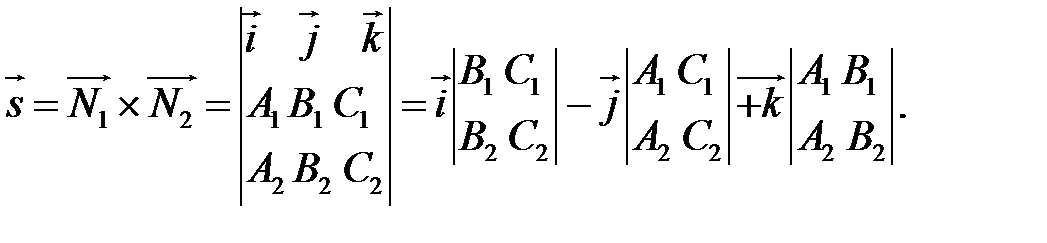

Рис.31.2
Тепер можна записати канонічне рівняння прямої, заданої загальним рівнянням:
 .
.






