Нехай є дві площини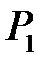 
і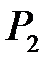 
, які в системі координат 
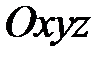задаються рівняннями 
: 
; 
: 
.
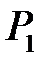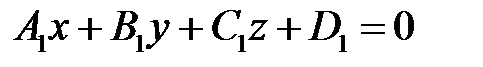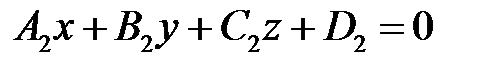Якщо ці площини паралельні, то їх нормальні вектори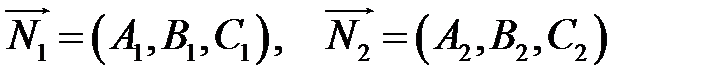 
колінеарні. Тому умовою паралельності двох площин є умова колінеарності цих векторів:
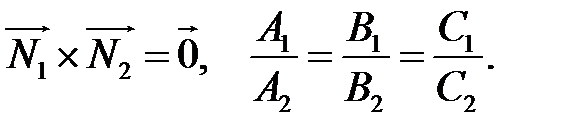
Коли площини не паралельні, то вони утворюють двогранний кут, що вимірюється гострим лінійним кутом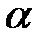 
або тупим 
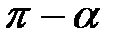(Рис.29.1). Один з лінійних кутів гострий або тупий співпадає з кутом 
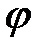між нормальними векторами площин.
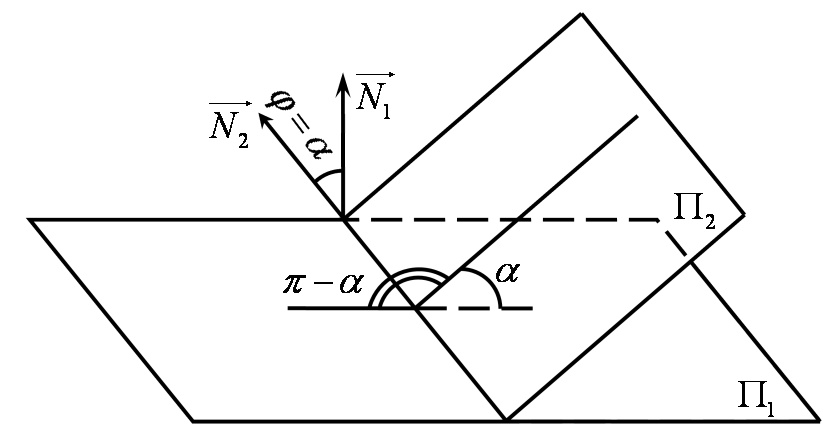
Рис.29.1
За формулою для визначення кута між векторами маємо:
Якщо результат, отриманий за формулою, додатній, то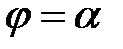 
, а якщо від'ємний, то 
.
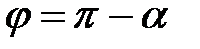Умовою перпендикулярності двох площин є умова перпендикулярності їх нормальних векторів:
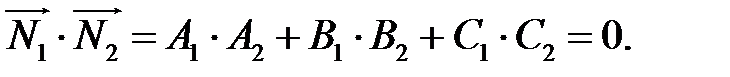
Розв'язання задач на складання рівнянь площини та взаємне розміщення площин у просторі
Задача 30.1. Скласти рівняння площини, що проходить через точку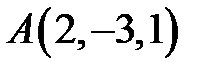 
перпендикулярно до вектора 
.
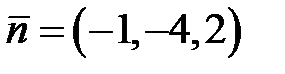