Статистическая величина описывает микросостояние системы, например вероятность его появления, вероятность определенной энергии или координаты частиц. Характеристиками макросостояния являютсятермодинамические величины и средние значения статистических величин, усредненных по микросостояниям фазового ансамбля. В общем случае термодинамическая величина зависит от текущего состояния системы и от пути перехода в это состояние.
Термодинамический потенциал зависит от состояния системы и не зависит от пути перехода в это состояние. Термодинамические потенциалы отличаются наборами своих аргументов, например, внутренняя энергия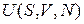 
; свободная энергия 
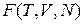. Потенциалами не являются работа A и теплота Q. Термодинамические потенциалы использовал Гиббс в 1874 г., термин ввел Пьер Дюгем в 1886 г.
Условие термодинамического равновесия. В термодинамике доказывается, что если система приходит к равновесию в результате некоторого процесса, то в равновесном состоянии экстремален тотпотенциал, аргументы которого не изменяются в ходе процесса.
Свойства потенциальной функции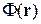 
:
1. Интеграл функции между начальным состоянием A и конечным B не зависит от формы пути
.
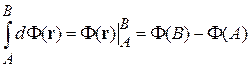2. При 
интеграл равен нулю. Следовательно, изменение потенциала при переходе системы из некоторого состояния по замкнутому пути в исходное состояние равно нулю.
3. Элементарное изменение потенциала является полным дифференциалом аргументов. Переход между бесконечно близкими значениями аргумента совершаем, проходя последовательно по участкам, параллельным ортам системы координат
.
Для потенциала Ф элементарное изменение обозначается знаком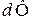 
, для не потенциала – 
. Рассмотрим ряд функций состояния.
Внутренняя энергия 
. Полная энергия микросостояния системы, то есть гамильтониан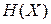 
, складывается из кинетической и потенциальной энергий всех частиц системы и зависит от микросостояния газа. Внутренняя энергия является полной энергией системы, усредненной по фазовому ансамблю
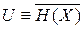, (2.31)
и выраженной через объем, число частиц и энтропию системы. Внутренняя энергия является функцией состояния, ее полный дифференциал
. (2.32)
Из первого начала термодинамики
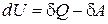, (2.33)
из определений энтропии
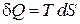
и работы
для равновесного, обратимого процесса при 
находим
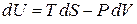. (2.34)
Давление Р равно средней силе, действующей со стороны газа на единицу площади стенки сосуда. Сравнение (2.34) с (2.32) дает
, (2.35)
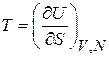. (2.36)
В состоянии равновесия внутренняя энергия минимальна.
Энтропия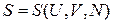 
– от греч. εντρέπω – «обращать», мера необратимости преобразования энергии. Для равновесного обратимого процесса увеличение энтропии газа пропорционально количеству полученного тепла
, (2.36а)
где использовано первое начало термодинамики. Понятие энтропии ввел Клаузиус в 1865 г.
Рудольф Клаузиус (1822–1888)
Энтропия является функцией состояния и выражается через внутреннюю энергию, объем и число частиц,
. (2.37)
Сравнивая с (2.36а)
,
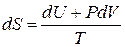получаем
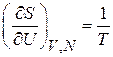, (2.37а)
. (2.37б)
В состоянии равновесия энтропия максимальна.
Свободная энергия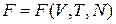 
является функцией состояния и выражается через объем, число частиц и температуру,
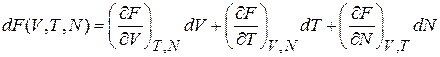. (2.38)
В термодинамике определяется в виде
, (2.39)
тогда
.
Подстановка (2.34)
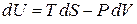
дает
. (2.40)
Сравниваем с (2.38) при , и находим
, (2.41)
. (2.42)
В состоянии равновесия свободная энергия минимальна.
Для установления физического смысла свободной энергии рассмотрим изотермический процесс. Из (2.40)
при 
с учетом получаем
.
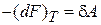Свободная энергия является частью внутренней энергии, которая при изотермическом процессе переходит в работу. Из (2.39)
следует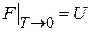 
– свободная энергия равна внутренней энергии при 
.
Связанная энергия равна разности между внутренней и свободной энергиями
.
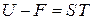Связанная энергия эточасть внутренней энергии, которая при изотермическом процессе не может быть превращена в работуи выделяется в виде теплоты. Понятия свободной и связанной энергий ввел Гельмгольц в 1847 г.
Герман Гельмгольц (1821–1894)
