Для частицы обобщенные координаты q и импульсы p связаны с энергией дисперсионным соотношением
.
Микросостояния с фиксированной энергией находятся в 2 f -мерном фазовом пространстве на гиперповерхности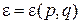 
. Число состояний внутри гиперповерхности получаем из (2.12)
при 
. (2.15)
Рассмотрим степенную зависимость энергии от импульса
,
где s и t – вещественные числа; p – модуль импульса. Фиксируем энергию и координаты, тогда в f -мерном импульсном пространстве получаем сферой радиусом
.
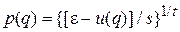Интеграл по импульсам в (2.15) равен объему f- мерного шара
.
Результат интегрируем по координатам области, ограниченной поверхностью 
, и из (2.15) в виде
получаем
. (2.16)
Если энергия частицы, находящейся в объеме 
, зависит от импульса и не зависит от координат
, 
,
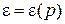тогда в (2.15)
интегрирования по координатам и импульсам разделяются. Получаем число состояний частицы с энергией ε
, (2.17)
где 
– объем импульсного пространства, ограниченный гиперповерхностью .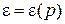
Для частицы с законом дисперсии
,
где s, t и u – вещественные числа, модуль импульса 
. Используем объем шара
,
и из (2.17) при 
получаем
. (2.18)
В частности, для 
:
: 
; (2.18а)
: 
; (2.18б)
: 
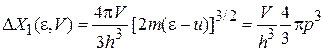, (2.18в)
где 
, 
, 
– длина, площадь и объем, занятые одномерным, двухмерным и трехмерным газом, соответственно. В (2.18а) множитель 2 учитывает два направления импульса одномерного движения.
