Система изолирована и энергия сохраняется
.
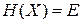Фазовый ансамбль находится в фазовом пространстве на гиперповерхности постоянной энергии, все ее точки равноправны. Вне гиперповерхности микросостояния отсутствуют. Следовательно, вероятность обнаружения системы в единице объема фазового пространства около точки X, или функция микроканонического распределения является дельта-функцией
. (2.7)
Плотность вероятности реализации микросостояний одинакова во всех точках гиперповерхности. Условие нормировки (2.4)
,
где 
, дает нормировочную постоянную
. (2.8)
Функцию 
выразим через энергетическую плотность состояний.
Энергетическая плотность состояний 
Набор возможных значений энергии системы называется энергетическим спектром. Газ в ограниченном объеме имеет дискретный спектр, зависящий от величины объема и от соотношения между энергией и импульсом частицы. На рисунке показан пример энергетического спектра. При макроскопическом объеме газа расстояние между уровнями мало и спектр квазинепрерывный. Для характеристики спектра используем энергетическую плотность уровней 
– число уровней в единичном интервале энергии. В классической физике уровень энергии соответствует микросостоянию, тогда – энергетическая плотность микросостояний. Выразим энергетическую плотность через распределение микросостояний по фазовому пространству.
Микросостояния с энергией 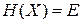находятся в фазовом пространстве на замкнутой гиперповерхности. Число микросостояний внутри гиперповерхности равно безразмерному объему фазового пространства
. (2.9)
При увеличении энергии на 
гиперповерхность сдвигается, объем фазового пространства внутри нее возрастает, число микросостояний увеличивается на
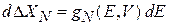. (2.10)
В результате энергетическая плотность состояний системы 
равна увеличению фазового объемапри возрастании энергии на единицу
. (2.11)
Приведенные соотношения применимы также к одной частице идеального газа. Значок Δ, использованный в (2.9) – (2.11), может далее упускаться для упрощения записей.
