Для изолированного газа энергия сохраняется, тогда
.
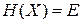Уравнение описывает в фазовом пространстве гиперповерхность 
с фиксированными значениями E, V, N. Формулу (2.10)
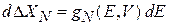
интегрируем и находим число микросостояний внутри гиперповерхности
. (2.43)
Из (2.8) и (2.11а)
,
,
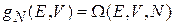получаем энергетическую плотность микросостояний
,
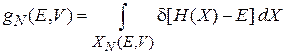и подставляем в (2.43)
.
Переставляем порядок интегрирований
.
Число микросостояний внутри гиперповерхности 
варьируем по объему при постоянной энергии. От объема зависит гамильтониан, тогда
,
.
В аргумент дельта-функции входят симметрично H и 
, заменяем
,
получаем
.
При вычислении внутреннего интеграла учтено
,
на нижнем пределе 
, поскольку 
.
Используем микроканоническое распределение (2.11б) в виде
,
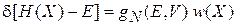тогда
.
Используем определение среднего для распределения 
.
Получаем изменение числа микросостояний с постоянной энергией при увеличении объема газа на единицу
. (2.44)
