Полученные соотношения для идеального газа применимы также к одной частице. Плотность состояний частицы равна числу состояний в единичном интервале энергии около значения ε
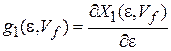. (2.22)
Для закона дисперсии
из (2.16)
находим
. (2.23)
В частности, для
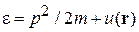
из (2.23) получаем
: 
, (2.24а)
: 
, (2.24б)
: 
, (2.24в)
где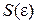 
– площадь, ограниченная кривой 
. В (2.24а) для множитель 2 учитывает два направления импульса.
Если энергия частицы не зависит от координат
,
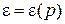тогда из (2.17)
и (2.22) следует
. (2.25)
Для дисперсии
,
где s, t и u – вещественные числа, из (2.18)
при 
находим
. (2.26)
В частности, для
из (2.26) получаем:
: 
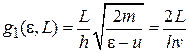, (2.27а)
: 
, (2.27б)
: 
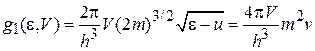, (2.27в)
где 
– скорость частицы. В двухмерной системе плотность состояний не зависит от энергии, поэтому спектр частицы эквидистантный.
Выразим термодинамические характеристики макросостояния – внутреннюю энергию U, давление P и энтропию S через статистическиехарактеристики микросостояний – гамильтониан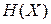 
, занимаемый объем фазового пространства 
и энергетическую плотность состояний 
.
