Найдем энергетическую плотность состояний гармонического осциллятора с частотой ω. Используем результат (П.2.4) для числа микросостояний с энергией ε
.
Из (2.11) при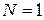 
получаем плотность спектра состояний частицы
.
Энергетическая плотность состояний обратно пропорциональна частоте, не зависит от объема и энергии. Результат согласуется со спектром осциллятора (П.2.4а)
,
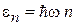где 
– интервал эквидистантного спектра. Число уровней в единичном интервале энергии равно 
.
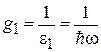Нормировочная постоянная микроканонического распределения
В выражение для нормировочной постоянной (2.8)
подставляем (2.10)
,
получаем
.
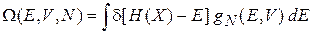Фильтрующее свойство дельта-функции снимает интеграл и дает
. (2.11а)
Следовательно, нормировочная постоянная микроканонического распределения равна энергетической плотности состояний.
