Для газа из N частиц, находящихся в элементе объема фазового пространства 
, число микросостояний равно безразмерному объему (2.2)
.
Интегрируем и получаем число микросостояний в объеме 
фазового пространства
.
Микросостояния с фиксированной энергией E находятся на гиперповерхности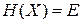 
, где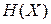 
– гамильтониан системы. Число состояний внутри гиперповерхности
. (2.12)
При отсутствии внешнего силового воздействия координаты и импульсы частиц не зависят друг от друга, тогда интегрирования разделяются
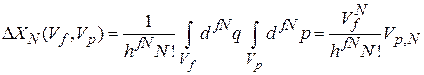, (2.13)
где
– объем сосуда, в котором находится газ;
;
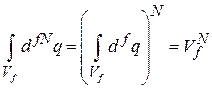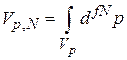– объем импульсного пространства, доступный для N частиц газа.
Для идеального изолированного классического газа с потенциальной энергией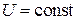 
и массами частиц m, не зависящими от направления, полная и кинетическая энергии постоянны и связаны с импульсами дисперсионным соотношением
.
В импульсном пространстве получаем уравнение сферы
.
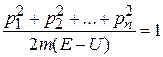Микросостояния идеального газа с полной энергией Е и потенциальной энергией 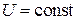находятся в импульсном пространстве на сфере радиусом 
. Импульсное пространство имеет размерность 
. Согласно примеру 2.1 объем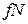 
-мерного шара радиусом p
.
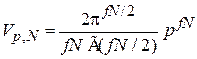Для газа из N частиц в объеме 
с полной энергией 
из (2.13)
получаем число микросостояний
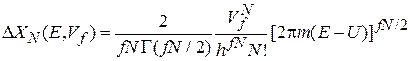. (2.14)
