Рассмотрим процесс приведения в тепловой контакт и перехода к термодинамическому равновесию первоначально теплоизолированных систем 1 и 2, показанных на рисунке. При выдвижении теплоизолирующего слоя перегородки a-b тепло перетекает между системами. Энергия всей системы сохраняется
,
тогда вариации энергий
.
Число микросостояний всей системы равно произведению числа микросостояний составляющих независимых систем
.
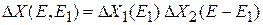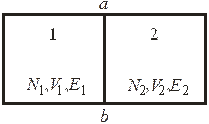
Теплоизолированные системы 1 и 2
При термодинамическом равновесии устанавливается наиболее вероятное состояние, в котором макросистема находится бόльшую часть времени, совершая кратковременные флуктуации. Фазовый ансамбль в своем движении по фазовому пространству последовательно проходит микросостояния. Максимальному временисоответствует максимальное число микросостояний, через которые проходит система. Накладываем условие экстремума на число микросостояний всей системы, тогда вариация
.
или для
в явной форме
.
С учетом 
и , находим
.
Аналогично ведет себя температура согласно общему началу термодинамики – при тепловом равновесии температура выравнивается во всех точках системы. Сопоставляем величины и для равновесной системы получаем
, (2.68)
где с учетом размерностей 
– тепловая энергия. При рассмотрении конкретных систем и сравнении результатов с формулами термодинамики будет показано, что k – постоянная Больцмана. Согласно (2.68) число микросостояний равно произведению энергетической плотности состояний на тепловую энергию. Следовательно, микросостояния фазового ансамбля создаются тепловой энергией.
Для газа из N атомов с энергией E в f -мерном пространстве с законом дисперсии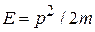 
подстановка (2.64а)
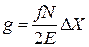
в (2.68) дает выражение энергии газа и средней энергии частицы через температуру
, 
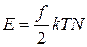. (2.69)
В результате установлен статистический смысл температуры, отсчитываемой по шкале Кельвина – температура пропорциональна средней кинетической энергии частицы.
В (2.65)
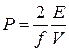
подставляем (2.69) и получаем известное в термодинамике уравнение идеального газа
,
где 
– концентрация частиц; k – постоянная Больцмана.
