А. Согласно теореме 
, следовательно
,
и сохраняется число микросостояний в единице объема при перемещении микросостояний по фазовому пространству. Каждое микросостояние описывает реальный объект, и число микросостояний не меняется. Тогда фазовый объем элемента ансамбля не изменяется с течением времени
,
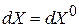изменяется лишь форма объема. Аналогично ведет себя объем несжимаемой жидкости. Учитываем
,
где J – якобиан преобразования между начальными 
и текущими X координатами, получаем
= 1. (2.6)
Модуль якобиана, связывающего начальные и текущие фазовые координаты, равен единице. Результат используется при проверке выполнения теоремы Лиувилля для конкретной системы.
При одномерном движении частицы в плоскости 
из (2.6) получаем
. (2.6а)
Б. Для стационарной системы функция распределения является макрохарактеристикой. Согласно теореме Лиувилля она не изменяется с течением времени, поэтому может зависеть только от интегралов движения. Если система как целое неподвижна и не вращается, то функция распределения зависит от полной энергии, то есть от гамильтониана:
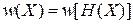. (2.6б)
В. Для равновесной изолированной системы
.
Система с равной вероятностью обнаруживается в любом из доступных микросостояний.
Г. Теорема не выполняется для диссипативных систем, т. е. при наличии трения и неупругих соударений. Диссипативная сила, действующая на тело со стороны среды, направлена против скорости движения тела относительно среды. Уравнения Гамильтона в виде (2.1) в этом случае не применимы.
