Равновесный газ описывается стационарным, то есть не зависящим от времени, гамильтонианом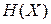 
и постоянными термодинамическими параметрами. Макросостояние реализуется фазовым ансамблем микросостояний. Это множество точек с течением времени движется по фазовому пространству. Закон их перемещения описывает теорема Лиувилля – при движении точек фазового ансамбля плотность микросостояний вдоль траектории остается постоянной и зависит от гамильтониана
, 
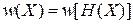. (2.5)
Аналогично течет несжимаемая жидкость, сохраняя свою плотность. Теорему доказал французский математик Лиувилль в 1838 г. Теорема используется для получения явного вида функции распределения состояний по фазовому пространству.
Жозеф Лиувилль (1809–1882)
Доказательство теоремы
Рассмотрим бесконечно малый объем фазового пространства в форме цилиндра с осью вдоль одной из обобщенных координат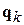 
. Основания цилиндра 
перпендикулярны оси, длина образующей 
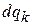. Микросостояния с плотностью 
входят в объем и выходят из него.
Для нахождения числа вошедших за 1с микросостояний представим микросостояние в виде точки на рисунке. Число точек в единице объема равно w. Если все точки двигаются со скоростью 
, то за 1с через сечение 
пройдут состояния, которые первоначально заполняли цилиндр с образующей, равной скорости. Умножаем объем цилиндра на плотность состояний, получаем число вошедших состояний
.
От точки к точке оси 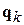меняется плотность микросостояний и их скорость, тогда число состояний, выходящих через сечение 
равно
,
где использовано
.
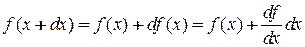Если плотность изменяется с течением времени, тогда в объеме появляются и исчезают состояния. За 1с в объеме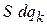 
появляется число состояний
.
Каждое состояние описывает реальную систему, поэтому число состояний сохраняется и выполняется уравнение баланса
«число появившихся состояний» =
= «число вошедших состояний» – «число вышедших состояний»:
.
Сокращаем подобные и получаем
.
Результат обобщаем на случай изменения всех 
координат фазового пространства
.
Раскрываем круглые скобки
.
Последняя скобка равна нулю согласно уравнениям Гамильтона (2.1)
, 
.
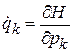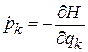Получаем уравнение Лиувилля
(2.5а)
Используем выражение для полной производной
,
получаем теорему Лиувилля
(2.5б)
– полная производная по времени от плотности микросостояний равна нулю. Следовательно, плотность микросостояний фазового ансамбля не изменяется при его движении.
Пример
Для одномерного движения свободной частицы запишем уравнение Лиувилля и найдем его решение. Сравним результат с решением уравнений Гамильтона.
Уравнение Лиувилля (2.5а)
для одномерного движения частицы с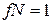 
имеет вид
. (П.2.2)
Для получения 
и 
используем гамильтониан свободной частицы
.
Из уравнений Гамильтона (2.1)
, 
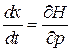
находим
, 
.
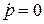Задаем начальные условия 
, 
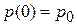. Решаем уравнения и получаем известные формулы равномерного движения
, 
, 
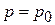. (П.2.3)
Подставляем (П.2.3) в (П.2.2)
и получаем уравнение Лиувилля
.
Уравнению удовлетворяет
,
где 
– распределение плотности вероятности обнаружения частицы в начальный момент времени.
Плотность вероятности обнаружения координаты и импульса частицы 
определяет траекторию и закон движения частицы в фазовом пространстве, как и уравнения Гамильтона. Если при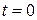 
для частицы заданы не начальные условия, а их распределение в фазовом пространстве , то динамика частицы описывается не уравнениями Гамильтона, а эволюционным уравнением Лиувилля (2.5а).
