Металлы первой группы таблицы Менделеева содержат в электронной оболочке один слабо связанный с атомом валентный электрон. При объединении атомов в кристаллическую решетку этот электрон становится свободным. В узлах кристаллической решетки металла остаются ионы, которые совершают тепловые колебания. Валентные электроны образуют идеальный газ с концентрацией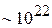 
см–3. В любом макроскопическом объеме имеется одинаковое число положительных и отрицательных зарядов, поэтому на электрон не действуют электростатические силы. Благодаря тепловому движению электрон хаотически перемещается от столкновения с ионом до столкновения с другим ионом. При нормальной температуре средняя скорость теплового движения ~100 км/с.
При термодинамическом равновесии процессы стационарные и вероятность b столкновения электрона за единицу времени не зависит от момента t. За время dt вероятность столкновения
.
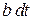Функция распределения времен свободного пробега w (t) равна вероятности того, что время свободного движения лежит в единичном интервале около значения t. Вероятность свободного движения до момента t и столкновения в следующий промежуток dt по теореме умножения вероятностей независимых событий равна
,
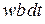и является уменьшением вероятности свободного движения при переходе от t к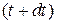 
. Для вероятности свободного движения получаем уравнение
.
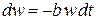Разделяем переменные
,
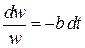интегрируем
,
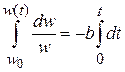где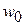 
– вероятность, что время свободного движения лежит в единичном интервале около нуля. Получаем
,
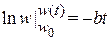потенцируем
.
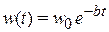Нормируем вероятность
,
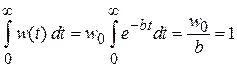получаем
, 
.
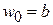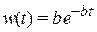Среднее время свободного пробега
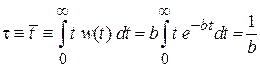(П.1.22)
обратно вероятности столкновения электрона за единицу времени. При нормальной температуре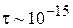 
с. В результате функция распределения времен свободного пробега
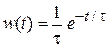. (П.1.23)
Следовательно, вероятность свободного движения в течение времени t уменьшается экспоненциально с ростом t.
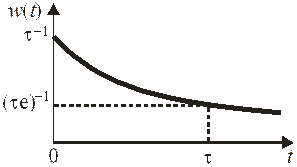
Среднеквадратичное время свободного пробега
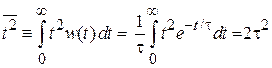(П.1.23а)
равно удвоенному квадрату среднего времени свободного пробега, где интеграл вычислен по частям.
