Пусть вероятность появления признака у одной частицы мала 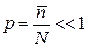 и общее число частиц велико
и общее число частиц велико 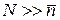 , тогда, если признак имеют в среднем
, тогда, если признак имеют в среднем 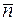 частиц, то его вероятность для n частиц
частиц, то его вероятность для n частиц
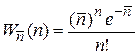 . (1.32)
. (1.32)
Результат получил Пуассон в 1837 г. на основе биномиального распределения.

Симеон Дени Пуассон (1781–1840)
Производящая функция. Используем (1.28) 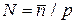 и производящую функцию биномиального распределения (1.27)
и производящую функцию биномиального распределения (1.27)
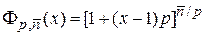 .
.
Учитываем 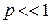 и
и
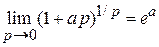 ,
,
где  . Получаем производящую функцию для распределения Пуассона
. Получаем производящую функцию для распределения Пуассона
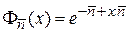 . (1.33)
. (1.33)
Выполняется нормировка (П1.16) 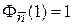 , тогда
, тогда
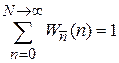 .
.
В (П.1.15)

подставляем (1.33), получаем
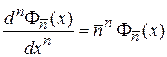 ,
,
находим распределение Пуассона (1.32)
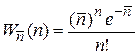 .
.
Среднеквадратичное число частиц и дисперсия. Из результатов для биномиального распределения (1.30) и (1.31)
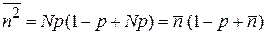 ,
,
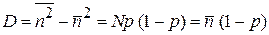
при 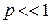 получаем
получаем
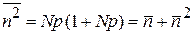 , (1.36)
, (1.36)
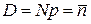 . (1.37)
. (1.37)
Для флуктуации 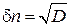 выполняется закон больших чисел – флуктуация относительно среднего значения равна корню квадратному из среднего значения
выполняется закон больших чисел – флуктуация относительно среднего значения равна корню квадратному из среднего значения
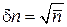 . (1.38)
. (1.38)
График распределения для 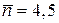 показан на рис. (б).
показан на рис. (б).
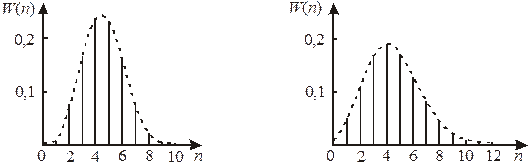
а б
Распределения биномиальное (а) и Пуассона (б) для N = 10, 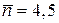 , р = 0,45
, р = 0,45
Сравнение графиков показывает погрешность, допускаемую распределением Пуассона (график б), вызванную не достаточно малым p и не достаточно большим N.






