Если некий признак имеют в среднем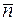 
частиц, то при большом числе частиц N и большом среднем 
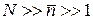и при относительно малом отклонении от среднего 
распределение Пуассона для вероятности признака у n частиц переходит в нормальное распределение, или распределение Гаусса:
. (1.40)
Условие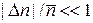 
позволяет считать n и 
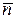квазинепрерывными величинами, тогда вероятность (1.40) становится плотностью вероятности
. (1.41)
Распределение получил Гаусс в 1809 г.
Карл Фридрих Гаусс (1777–1855)
Доказательство (1.40)
Условие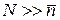 
означает 
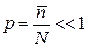и выполнение распределения Пуассона
.
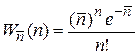Логарифмируем
.
При 
используем формулу Стирлинга для факториала (рассматривалась в курсе ММФ)
,
тогда
.
Получаем
.
Вводим отклонение от среднего 
, тогда
.
Для распределения Гаусса выполняется 
. Разлагаем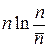 
по степеням малой величины 
и сохраняем первые два слагаемых разложения, считая остальные несущественными:
.
Находим
.
Потенцируем результат и, используя 
, заменяем 
, и получаем (1.40)
.
Характеристическая функция. Подставляем распределение Гаусса (1.41) для непрерывной случайной величины
в определение характеристической функции (1.14)
,
где сделана замена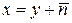 
. Используем интеграл из курса ММФ
,
находим характеристическую функцию для нормального распределения
. (1.42)
Выполняется (1.16) 
, следовательно, распределение Гаусса (1.41) нормировано
. (1.43)
Среднее число частиц с неким признаком получаем из (1.17) и (1.42)
.
Тождество означает, что в нормальном распределении (1.41) величина 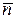является средним числом частиц с неким признаком.
Среднее квадратичное числа частиц находим аналогично
. (1.44)
Результат (1.44) совпадает с выражением для распределения Пуассона.
Дисперсия числа частиц получается из (1.44)
, (1.45)
дисперсия равна среднему числу частиц.
Из (1.41) и (1.45) получаем плотность вероятности в виде
. (1.47)
Функция показана на рис. 1.2.
Рис. 1.2. Распределение Гаусса, 
Центральная предельная теорема – при суммировании большого числа независимых случайных величин, имеющих различные распределения, результирующее распределение близко к распределению Гаусса.
Теорема обосновывает применимость нормального распределения к многочисленным случайным процессам. Теорему доказал Ляпунов в 1901 г.
Александр Михайлович Ляпунов (1857–1918)
