1. Знайти координати вершин, півосі, півфокусну відстань, ексцентриситет і рівняння асимптот гіпербол, побудовати їх графіки.
1) 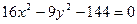 , 2)
, 2) 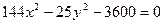 , 3)
, 3) 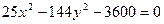 .
.
2. Скласти канонічне рівняння гіперболи, фокуси якої розміщені на осі ОХ, якщо
1) а=5, b=3;
2) 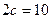 і 2b=8;
і 2b=8;
3) 2b=6 і 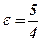 ;
;
4) рівняння асимптот 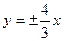 і
і  .
.
3. Скласти канонічне рівняння гіперболи, дійсна вісь якої лежить на осі ОХ, якщо гіпербола проходить через точки 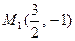 і
і 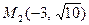 .
.
4. Записати рівняння гіперболи, дійсна вісь якої дорівнює 6, і відстань фокусами дорівнює 10, записати рівняння спряженої гіперболи. Побудувати їх графіки.
5. Знайти центр, півосі, півфокусну відстань, ексцентриситет і канонічне рівняння гіпербол:
1)  ;
;
2)  ;
;
3) 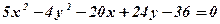 . Побудувати ці гіперболи.
. Побудувати ці гіперболи.
Вказівка: необхідно виділити повні квадрати змінних і знайти новий початок координат, що відповідатиме паралельному переносу системи координат в новий центр (див. розв’язану аналогічну задачу 4 в попередньому параграфі для еліпса).
6. Знайти точки перетину гіперболи  з прямою
з прямою 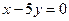 .
.
7. Відомо, що гіпербола проходить через фокуси еліпса 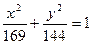 , а її фокуси знаходяться у вершинах еліпса. Скласти рівняння гіперболи.
, а її фокуси знаходяться у вершинах еліпса. Скласти рівняння гіперболи.
8. Ексцентриситет гіперболи, яка має спільні фокуси з еліпсом  , дорівнює 1,2. скласти рівняння цієї гіперболи.
, дорівнює 1,2. скласти рівняння цієї гіперболи.
9. Знайти площу прямокутника, вершини якого містяться в точках перетину гіперболи 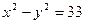 і кола
і кола  .
.
10. Гіперболи задані рівняннями  і
і 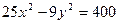 . Знайти кут між їхніми асимптотами, які розміщені в першій чверті.
. Знайти кут між їхніми асимптотами, які розміщені в першій чверті.
Відповіді: 1. 1)  ; 2)
; 2) 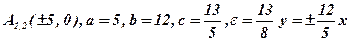 ;
;
3) 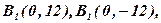
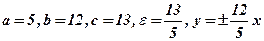 .
.
2. 1) 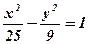 ; 2)
; 2) 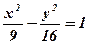 ; 3)
; 3) 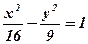 ;
;
4)  . 3.
. 3.  . 4.
. 4. 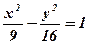 ,
, 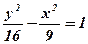 . 5. 1)
. 5. 1) 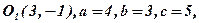
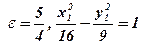 ;
;
2) 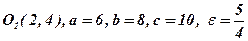
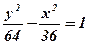 ;
;
3) 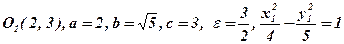 .
.
6.  ,
, 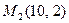 . 7.
. 7. 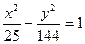 . 8.
. 8. 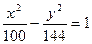 .
.
9.112. 10..




