1. За рівняннями а) 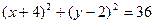 , б)
, б) 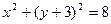 , в)
, в) 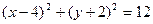 знайти центри та радіуси кіл.
знайти центри та радіуси кіл.
2. Скласти рівняння кола з центром у точці С і радіусом R: 1) С(-6,-3), R=5; 2) C(1,-2),  ; 3) C(2,0), R=3; 4) C(0,-1), R=1,5.
; 3) C(2,0), R=3; 4) C(0,-1), R=1,5.
3. Для поданих рівнянь кіл знайти координати їх центрів і радіуси: 1) 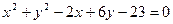 ;
;
2)  ; 3)
; 3)  .
.
4. Скласти рівняння кола, якщо кінці його діаметра містяться у точках А(-3,-1) і В(1,5).
5. Скласти рівняння кола з центром в точці О(0,0), яке дотикається прямої  .
.
6. Записати рівняння кола з радіусом рівним 13, яке проходить через точки А(3,-1), і В(-4,-8).
7. Трикутник заданий вершинами L(-3,6), M(-1,10), N(6,9). Записати рівняння описаного навколо DLMN кола.
8. Написати рівняння дотичної до кола 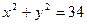 в точці М(5,3).
в точці М(5,3).
9. Коло задане рівнянням 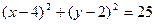 . Скласти рівняння дотичної до кола в точці М(0,1).
. Скласти рівняння дотичної до кола в точці М(0,1).
10. Знайти відстань між центрами кіл  і
і  .
.
Відповіді: 1. а) С(-4,2), R=6; б) С(0,-3),  ; в) С(4,-2),
; в) С(4,-2), 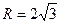 . 2. 1)
. 2. 1) 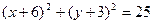 ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  .
.
3. 1) 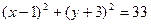 ; 2)
; 2)  ; 3)
; 3) 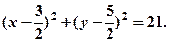 . 4.
. 4. 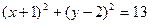 .
.
5. 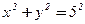 .
.
6. 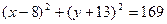 або
або 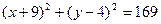 .
.
7.  . 8.
. 8. 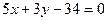 .
.
9. 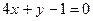 . 10. 10.
. 10. 10.
Еліпс
Означення. Еліпсом називається множина точок площини, сума відстаней яких від двох заданих точок, що називаються фокусами, є величина стала і дорівнює 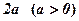 .
.
Позначимо фокуси 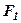 і
і 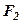 . Припустимо, що відстань
. Припустимо, що відстань 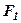
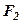 =
= 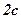 – фокусна відстань. Щоб отримати канонічне рівняння еліпса розмістимо
– фокусна відстань. Щоб отримати канонічне рівняння еліпса розмістимо 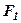 і
і 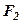 на осі
на осі 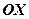 , симетрично щодо початку координат. Тоді фокуси матимуть координати
, симетрично щодо початку координат. Тоді фокуси матимуть координати 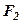
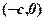 і
і 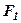
 (див. рис. 24).
(див. рис. 24).
Нехай M ( x, y ) – довільна точка еліпса. Позначимо через r 2 і r 1 – відстані від точки M до фокусів. Згідно з означенням еліпса.
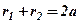 . (38)
. (38)
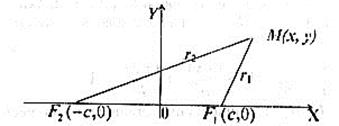
Рис. 24.
Підставимо в (38)  ,
, 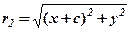 і звільнимось від ірраціональності, піднісши обидві частини до квадрата, отримаємо:
і звільнимось від ірраціональності, піднісши обидві частини до квадрата, отримаємо:

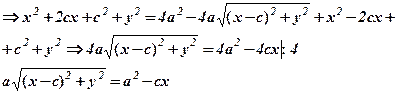
(підносимо до квадрата обидві частини) 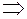

Позначимо: 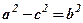 , отримаємо канонічне рівняння еліпса:
, отримаємо канонічне рівняння еліпса:
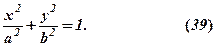
Відмітимо, що за відомою властивістю трикутника (сума двох сторін більша третьої) із 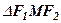 маємо
маємо 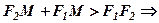
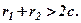 Оскільки
Оскільки 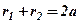 , то
, то 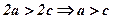 , а тому
, а тому
 (*)
(*)
Для побудови еліпса зауважимо, що якщо точка  належить еліпсу, тобто задовольняє рівняння (39), то точки
належить еліпсу, тобто задовольняє рівняння (39), то точки  теж задовольняють це рівняння: із
теж задовольняють це рівняння: із
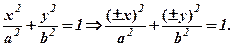
Точки 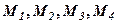 – розміщені симетрично відносно осей координат. Отже, еліпс – фігура симетрична відносно координатних осей. Тому досить побудувати графік в першій чверті, а тоді симетрично продовжити його.
– розміщені симетрично відносно осей координат. Отже, еліпс – фігура симетрична відносно координатних осей. Тому досить побудувати графік в першій чверті, а тоді симетрично продовжити його.
З (39) знаходимо 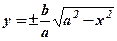 , для І -ої чверті
, для І -ої чверті 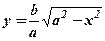 .
.
Якщо 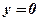 , то
, то 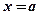 . Якщо ж
. Якщо ж  , то
, то  . Точки
. Точки 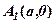 і
і 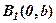 , а також симетричні з ними
, а також симетричні з ними 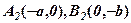 – вершини еліпса, точка
– вершини еліпса, точка  – центр еліпса,
– центр еліпса,  – велика вісь,
– велика вісь,  – мала вісь еліпса. Якщо
– мала вісь еліпса. Якщо  І чверті, то із
І чверті, то із 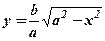 випливає, що при зростанні
випливає, що при зростанні 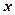 від
від  до
до  значення
значення  спадає від
спадає від  до
до  . Зображення еліпса на рис. 25.
. Зображення еліпса на рис. 25.
Величина відношення міжфокусної відстані до великої осі називається ексцентриситетом еліпса і, після скорочення на 2, позначається  . Значення ексцентриситета характеризує ступінь “сплющенності” еліпса. Якщо
. Значення ексцентриситета характеризує ступінь “сплющенності” еліпса. Якщо 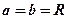 , то
, то  – маємо коло. Якщо ж
– маємо коло. Якщо ж  , то
, то 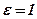 – еліпс вироджується у відрізок. В невироджених випадках
– еліпс вироджується у відрізок. В невироджених випадках 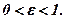 Для фокальних радіусів наведемо без доведення такі формули:
Для фокальних радіусів наведемо без доведення такі формули:
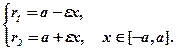 (**)
(**)
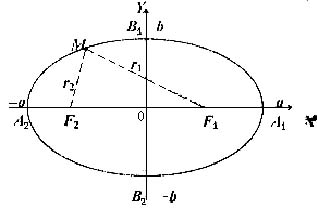
Рис. 25.
Еліпс можна побудувати механічним способом. Із канонічного рівняння знаходимо півосі  і
і  , тоді обчислюємо
, тоді обчислюємо  – півфокусну відстань. Будуємо фокуси
– півфокусну відстань. Будуємо фокуси 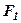 і
і 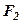 на відстані один від одного
на відстані один від одного 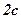 . Кінці нерозтяжної нитки довжиною
. Кінці нерозтяжної нитки довжиною  закріпляємо в точках
закріпляємо в точках 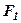 і
і 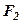 . Натягуючи вістрям олівця нитку, водимо вістрям по площині таким чином, щоб нитка ковзала по вістрю. Олівець при цьому опише півеліпс. Відтягуючи нитку в протилежну сторону, накреслимо другу половину еліпса.
. Натягуючи вістрям олівця нитку, водимо вістрям по площині таким чином, щоб нитка ковзала по вістрю. Олівець при цьому опише півеліпс. Відтягуючи нитку в протилежну сторону, накреслимо другу половину еліпса.
Задача 1. Задано еліпс рівнянням 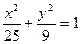 і точки М0(4;1,8), М1(3;2,4). Необхідно:
і точки М0(4;1,8), М1(3;2,4). Необхідно:
1) переконатись, що точки М0 і М1 лежать на еліпсі;
2) знайти півосі еліпса та координати його фокусів;
3) побудувати еліпс і точки М0 і М1;
4) знайти відстань від точки М0 до фокусів;
5) упевнитись, що сума цих відстаней дорівнює довжині великої осі;
6) знайти ексцентриситет еліпса.
Розв’язання. 1) Підставимо координати x=4; y=1,8 точки М0 в ліву частину рівняння еліпса:
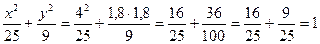 – точка М0 лежить на еліпсі. Аналогічно для М1(3;2,4):
– точка М0 лежить на еліпсі. Аналогічно для М1(3;2,4):
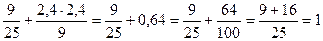 – точка М1 лежить на еліпсі.
– точка М1 лежить на еліпсі.
2) З канонічного 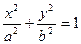 і даного рівняння
і даного рівняння 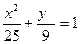 еліпса випливає
еліпса випливає  З рівності (*) цього параграфа
З рівності (*) цього параграфа 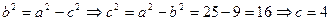 – півфокусна відстань. Координати фокусів F1(4;0) і F2(-4;0).
– півфокусна відстань. Координати фокусів F1(4;0) і F2(-4;0).
3)
Відкладемо значення півосі 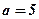 симетрично відносно точки О(0,0) на осі ОХ. Аналогічно b=3 відкладемо на осі ОУ.
симетрично відносно точки О(0,0) на осі ОХ. Аналогічно b=3 відкладемо на осі ОУ.
4) Знайдемо фокальні радіуси точки М0 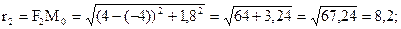
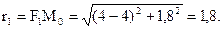
5) Знайдемо суму  , що відповідає означенню еліпса.
, що відповідає означенню еліпса.
6) Ексцентриситет знаходиться за формулою 
Задача 2. Знайти осі, вершини і фокуси еліпса 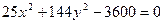 . Побудувати еліпс.
. Побудувати еліпс.
Розв’язання. Зведемо дане рівняння до канонічного вигляду (див. рівняння (39)), перенесемо вільний член вправо і почленно розділимо на нього всю рівність
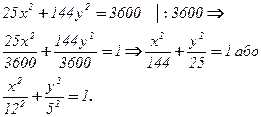
Порівнюючи останнє рівняння з рівнянням (39), маємо 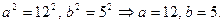 Звідси знаходимо осі еліпса 2а=24, 2b=10 і координати вершин А1(12,0), А2(-12,0), В1(0,5), В2(0,-5). Далі із формули
Звідси знаходимо осі еліпса 2а=24, 2b=10 і координати вершин А1(12,0), А2(-12,0), В1(0,5), В2(0,-5). Далі із формули 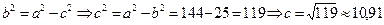 . Отже, фокусами еліпса є точки F1(
. Отже, фокусами еліпса є точки F1(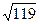 ,0) і F2(
,0) і F2(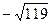 ,0). Для побудови еліпса відкладаємо на осях ОХ і ОУ вершини А1, В1, А2, В2 відповідно і з’єднуємо їх плавною лінією (див. попередню задачу).
,0). Для побудови еліпса відкладаємо на осях ОХ і ОУ вершини А1, В1, А2, В2 відповідно і з’єднуємо їх плавною лінією (див. попередню задачу).
Зауваження. Якщо у канонічному рівнянні 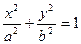 більшою піввіссю буде b>a, то фокуси еліпса будуть розміщені на осі ОУ і тоді
більшою піввіссю буде b>a, то фокуси еліпса будуть розміщені на осі ОУ і тоді 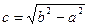 .
.
Задача 3. Знайти осі, вершини і фокуси еліпса  .
.
Розв’язання. Зведемо рівняння до канонічного 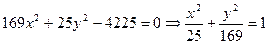 ,
, 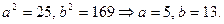 Вершини еліпса в точках А1(5,0), В1(0,13), А2(-5,0) і В2(0,-13). Будуємо вершини на координатних осях і з’єднаємо плавною лінією (див рис.). Оскільки в даному випадку b=13 більше ніж
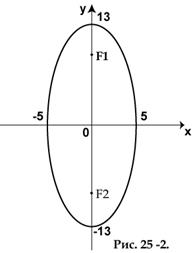
Вершини еліпса в точках А1(5,0), В1(0,13), А2(-5,0) і В2(0,-13). Будуємо вершини на координатних осях і з’єднаємо плавною лінією (див рис.). Оскільки в даному випадку b=13 більше ніж 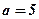 , то еліпс витягнутий вдовж осі OY і фокуси теж будуть на осі OY, знаходимо півфокусну відстань
, то еліпс витягнутий вдовж осі OY і фокуси теж будуть на осі OY, знаходимо півфокусну відстань  Фокуси в точках
Фокуси в точках 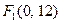 і
і 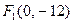 (див. рис. 25-2)
(див. рис. 25-2)
Задача 4. Довести, що рівняння

описує еліпс. Знайти координати центра, півосі, півфокусну відстань, ексцентриситет. Побудувати еліпс.
Розв’язання. Зведемо рівняння до канонічного вигляду. Спочатку згрупуємо по кожній із змінних і виділимо повний квадрат
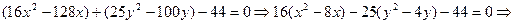
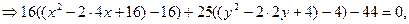
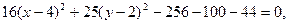
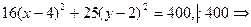
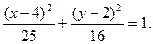
Позначимо  Зроблену заміну змінних будемо розглядати як перетворення прямокутних координат x і y із системи XOY в нові координати
Зроблену заміну змінних будемо розглядати як перетворення прямокутних координат x і y із системи XOY в нові координати 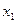 і
і 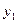 системи
системи  шляхом паралельного перенесення координатних осей, де новий початок знаходиться в точці
шляхом паралельного перенесення координатних осей, де новий початок знаходиться в точці 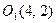 . В новій системі координат
. В новій системі координат  рівняння еліпса приймає канонічний вигляд
рівняння еліпса приймає канонічний вигляд

З канонічного рівняння  ,
, 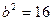 ,
, 
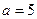 ,
,  ,
, 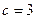 ,
, 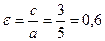 . Побудуємо в системі XOY точку
. Побудуємо в системі XOY точку 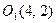 - новий початок координат, проведемо через
- новий початок координат, проведемо через 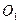 нові осі
нові осі  і
і 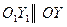 . В системі
. В системі  будуємо еліпс за отриманим канонічним рівнянням, тобто по
будуємо еліпс за отриманим канонічним рівнянням, тобто по  відкладаємо вліво і вправо відносно
відкладаємо вліво і вправо відносно 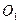 півосі
півосі 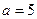 , а по
, а по 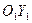 - аналогічні півосі
- аналогічні півосі  (див рисунок).
(див рисунок).







