Криві другого порядку
Рівняння вигляду
де хоча б один з коефіцієнтів 
або 
відмінний від нуля, називається алгебраїчним рівнянням першого порядку, або першого степеня відносно змінних 
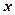і 
.
Рівняння (35) завжди описує пряму лінію.
Алгебраїчним рівнянням другого порядку називається всяке рівняння вигляду
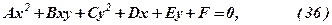
де хоча б один з коефіцієнтів 
.
Лінії, координати точок яких задовольняють рівняння (36) називаються лініями другого порядку. До ліній другого порядку відносяться: еліпс (зокрема коло), гіпербола, парабола. Вони описуються рівнянням вигляду (36). Однак не кожне рівняння другого порядку завжди описує одну із згаданих ліній. Може, наприклад, вийти так, що рівняння вигляду (36) описує пару прямих ліній або не визначає жодного реального об’єкту.
