Нехай задана кругова конічна поверхня, необмежена в обидві сторони від вершини. Внаслідок різних перетинів цієї поверхні і площини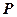 
можна отримати криві другого порядку (див. рис. 30).
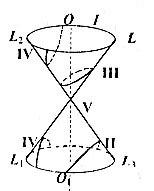
Рис. 30.
1. Якщо площина 
- осі конічної поверхні, але не проходить через її вершину, то в перетині буде коло 
.
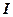2. Площина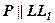 
- одній з твірних, тоді в перетині матимемо параболу 
.
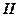3. Площина 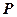перетинає конічну поверхню під кутом до її осі 
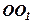, але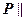 
жодній з твірних, тоді в перетині буде еліпс 
.
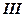4. 
, в перетині - гіпербола 
.
Вироджені випадки:
5. і проходить через вершину конічної поверхні, в перетині є точка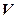 
.
6. Площина 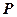проходить через вісь 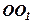, в перетині пара прямих, що перетинаються, наприклад, 
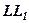і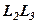 
.
Першим, хто розглядав криві другого порядку, як конічні перетини був древньогрецький математик Аполлоній (прибл. 262 – 190 роки до н.е.). Його праця “Конічні перетини” мала великий вплив на розвиток науки нових часів – астрономії, механіки, оптики; із його положень виходили французькі математики Р.Декарт (1596 – 1650) і П.Ферма (1601 – 1665) при створенні аналітичної геометрії.
