Рассмотрим более подробно критерий Сэвиджа, введенный выше соотношением (4.7). С помощью обозначений
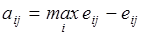(4.14)
и
(4.15)
формируется оценочная функция
(4.16)
и строится множество оптимальных вариантов решения
 |
E 0= 
. (4.17)
Для понимания этого критерия определяемую соотношением (4.14) величину 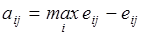можно трактовать как максимальный дополнительный выигрыш, который достигается, если в состоянии Fj вместо варианта Ei выбрать другой, оптимальный для этого внешнего состояния вариант. Мы можем, однако, интерпретировать аij, и как потери (штрафы), возникающие в состоянии Fj при замене оптимального для него варианта на вариант Ei. Тогда определяемая соотношением (4.15) величина eir представляет собой – при интерпретации аij в качестве потерь – максимальные возможные (по всем внешним состояниям Fj, (j =1,..., n) потери в случае выбора варианта Ei. Теперь, согласно (4.16) и (4.17), эти максимально возможные потери минимизируются за счет выбора подходящего варианта Ei.
Соответствующее S -критерию правило выбора теперь интерпретируется так:
Каждый элемент матрицы решений || еij || вычитается из наибольшего результата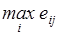 
соответствующего столбца.
Разности aij образуют матрицу остатков || aij ||. Эта матрица пополняется столбцом наибольших разностей еir. Выбираются те варианты Еi 0, в строках которых стоит наименьшее для этого столбца значение.
По выражению (4.16) оценивается значение результатов тех состояний, которые, вследствие выбора соответствующего распределения вероятностей, оказывают одинаковое влияние на решение. С точки зрения результатов матрицы || еij || S -критерий связан с риском, однако, с позиций матрицы || aij ||, он от риска свободен. В остальном к ситуации принятия решений предъявляются те же требования, что и в случае ММ-критерия.
