Чтобы прийти к однозначному и по возможности наивыгоднейшему варианту решения даже в том случае, когда каким-то вариантам решений Ei могут соответствовать различные условия Fj, можно ввести подходящие оценочные (целевые) функции. При этом матрица решений || eir ||сводится к одному столбцу. Каждому варианту Ei приписывается, таким образом, некоторый результат eir, характеризующий, в целом, все последствия этого решения. Такой результат мы будем в дальнейшем обозначать тем же символом eir.
Процедуру выбора можно теперь представить по аналогии с применением критерия (4.1). Возникает, однако, проблема, какой вложить смысл в результат eir. Если, например, последствия каждого из альтернативных решений характеризовать комбинацией из его наибольшего и наименьшего результатов, то можно принять
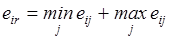. (4.2)
Из сказанного вытекает способ построения оценочных функций, приводимый в табл. 4.2. Наилучший в этом смысле результат имеет вид
. (4.3)
Теперь решение можно снова искать в соответствии с критерием (4.1). Формируя таким образом желаемый результат, конструктор исходит из компромисса между оптимистическим и пессимистическим подходами.
Рассмотрим теперь некоторые: другие оценочные функции, которые в данном примере мог бы выбрать конструктор, а также соответствующие им исходные позиции.
Таблица 4.2.
Построение оценочных функций
| E 1 | e 1 n |
| E 2 | e 2 n |
| E 3 | e 3 n |
| . . . | . . . |
| Ej | emn |
| . . . | . . . |
| Em | emn |
Оптимистическая позиция:
. (4.4)
Из матрицы результатов решений еij (табл. 4.1) выбирается вариант (строка), содержащий в качестве возможного следствия наибольший из всех возможных результатов. Наш конструктор становится на точку зрения азартного игрока. Он делает ставку на то, что. выпадет наивыгоднейший случай, и исходя из этого выбирает размеры изделия.
Позиция нейтралитета:
. (4.5)
Конструктор исходит из того, что все встречающиеся отклонения результата решения от «среднего» случая допустимы, и выбирает размеры, оптимальные с этой точки зрения.
Пессимистическая позиция:
. (4.6)
Конструктор исходит из того, что надо ориентироваться на наименее благоприятный случай и приписывает каждому из альтернативных вариантов наихудший из возможных результатов. После этого он выбирает самый выгодный вариант, то есть ожидает наилучшего результата в наихудшем случае. Для каждого иного внешнего состояния результат может быть только равным этому или лучшим.
Позиция относительного пессимизма:
. (4.7)
Для каждого варианта решения конструктор оценивает потери в результате по сравнению с определенным по каждому варианту наилучшим результатом, а затем из совокупности наихудших результатов выбирает наилучший согласно представленной оценочной функции.
Таблица 4.3.
Влияние вида оценочных функций на выбор размеров кабеля
| Уравнение | Оценочная функция | Результат |
| (4.6) | 
| 
|
| (4.5) | 
| 
|
| (4.7) | 
| 
|
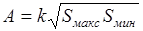
| (4.4) | 
| 
|
Ряд таких оценочных функций можно было бы продолжить. Некоторые из них получили широкое распространение в хозяйственной деятельности. Так, если условия эксплуатации заранее не известны, ориентируются обычно на наименее благоприятную ситуацию. Это соответствует оценочной функции (4.6). Нередко используются также функции (4.6) и (4.7).
В табл. 4.3 показан пример выбора сечения А кабеля при неизвестной токовой нагрузке S с использованием всех четырех вышеназванных оценочных функций. Константа k здесь одна и та же для всех четырех случаев. Отметим, что результаты зависят только от Sмакс и Sмин, т. е. от максимальной и минимальной токовых нагрузок.
Приведенные результаты существенно различаются. Они упорядочены таким образом, что влияние минимальной токовой нагрузки Sмин нарастает от строки к строке, т. е. получающиеся сечения становятся все меньше и меньше. Решение при этом становится все более оптимистичным. При этом выбор критерия определяется исключительно позицией конструктора. Поясним эти положения.
Влияние исходной позиции конструктора на эффективность результата решения можно интерпретировать, исходя из наглядных представлений. Простейшим здесь является графическое изображение на плоскости, для чего мы временно ограничимся случаем с двумя (п =2) внешними состояниями при т вариантах решения. Полезно, разумеется, чтобы мы уяснили для себя и, руководствуясь дальнейшими построениями, рассмотрели самостоятельно, как обобщается изложенное на случай большего, чем два, числа состояний, особенно на случай п =3,графически труднее представимый, но хорошо интерпретируемый в пространстве.
Введем теперь прямоугольную систему координат, откладывая по оси абсцисс значения результата решения еi 1, соответствующие внешнему состоянию F1 а по оси ординат – значения еi 2, соответствующие состоянию F 2, i= 1,..., т. В этом случае каждый вариант решения Ei, соответствует точке (ei 1, ei 2 ), i= 1,... т, на плоскости. Точку с координатами 
мы назовем утопической точкой (УТ). Смысл этого названия в том, что координаты всех точек 
,соответствующих вариантам решений 
не могут быть больше, чем у точки УТ, и что УТ встречается среди этих т точек только в том редком, идеальном случае, когда существует вариант решения, дающий максимальный результат для каждого из (двух) возможных внешних состояний. Аналогичное значение имеет и так называемая антиутопическая точка (АУТ), имеющая координаты 
координаты всех точек , соответствующих вариантам решений , не могут быть меньше, чем у точки АУТ. Отсюда следует, что все m точек лежат внутри прямоугольника, стороны которого параллельны координатным осям, а противоположные вершины – точки УТ и АУТ;мы называем этот прямоугольник полем полезности решений (рис. 4.1).
Теперь, чтобы сравнить варианты решений с точки зрения их качества, назовем вариант Ei не худшим, чем вариант Еj если для соответствующих точек 
и 
выполняются неравенства 
и 
. Причем Ei считается лучшим, чем Ej, если хотя бы одно из этих двух неравенств является строгим.
Очевидно, что при таком определении не любые два варианта решений допускают сравнение в том смысле, что один из них оказывается лучше другого. (Может случиться, что для точек и , соответствующих вариантам Ei и Ej выполняются, например, неравенства 
и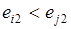 
). На математическом языке это означает, что на множестве вариантов решений установлено так называемое отношение частичного порядка. Это отношение частичного порядка обладает рядом свойств, хорошо усматриваемых на рис. 4.1. Выберем в поле полезности произвольную точку, которую будем называть. рассматриваемой (РТ). С помощью прямых, параллельных координатным осям, разобьем плоскость на четыре части и обозначим их I, II, III и IV. В рассматриваемом нами двумерном случае каждая из этих частей имеет вид (бесконечного) прямоугольника; в случае произвольной размерности они превращаются в так называемые конусы.
Рассматривая положение точек поля полезности относительно этих четырех.конусов, можно в общем случае сказать следующее. Все точки из конуса I в смысле введенного выше частичного порядка лучше, чем рассматриваемая точка РТ. Поэтому мы называем конус I конусом предпочтения. Соответственно все точки из конуса III хуже точки РТ, и мы будем называть область III антиконусом. Таким образом, оценка качества точек из этих двух конусов в сравнении с точкой РТ проста и однозначна. Оценкаже точек в отмеченных штриховкой конусах II и IV является неопределенной, вследствие чего их называют областями неопределенности. Для этих точек оценка получается только с помощью выбранного критерия принятия решения. В случае m вариантов решений и п внешних состояний Fi,..., Fn критерий принятия решения можно представить в виде
или
.
Функция п переменных К. характеризует соответствующий критерий и задает одновременно оценочную функцию. Для анализа критерия рассмотрим, полагая ei 1= x 1, еi 2 =х 2,..., еin=хп, функцию К на всем n -мерном пространстве Rn. Тогда каждому значению действительного параметра k посредством равенства
K (x 1,..., xп)= k
ставится в соответствие некоторая гиперповерхность в пространстве Rn, называемая нами поверхностью уровня, соответствующей значению k. В двумерном случае, интересующем нас ввиду его наглядности, мы специально полагаем ei 1= x 1= u, и еi 2 =х 2 =v, отождествляя тем самым еi 1-ось с u -осью, а еi 2-ось с v -осью, и с помощью равенства
K (u, v)= k.
Получаем в этом случае на плоскости (и, v) кривую, называемую линией уровня, соответствующей значению k. При фиксированном уровне k уравнение K (и,v) =k определяет функциональную зависимость между переменными и и v, называемую функцией предпочтения; так же называют и соответствующую кривую на плоскости (u, v).
Рассмотрим, например, оценочную функцию (4.5). При еi 1 =и и еi 2 =v получаем для т=2 семейство функций предпочтения, зависящих от параметра k:
(u + v)/ n = k.
При графическом изображении это выражение дает прямые, параллельные биссектрисе второго и четвертого квадрантов плоскости (и,v). Поскольку рассматриваемому критерию, в соответствии с которым путем оптимального выбора решения максимизируется среднее значение всех возможных результатов, отвечает нейтральная в известном смысле позиция принимающего решение, мы приписываем название «нейтральной» и соответствующей функции предпочтения (рис. 4.2). Выберем теперь на какой-либо линии уровня этого критерия произвольную точку РТ и проведем через нее «осевой крест», разбивающий плоскость на описанные выше четыре квадранта – конус предпочтения, антиконус и конусы неопределенности.
 |
Все точки из областей неопределенности, лежащие справа и выше этой линии уровня, в смысле нашего критерия лучше точек, лежащих слева и ниже. Сказанное справедливо и для функций предпочтения любого другого критерия. Всякая функция (кривая) предпочтения объединяет все точки фиксированного уровня; оправа и выше ее располагаются все лучшие точки, то есть точки более высокого уровня, а слева и ниже – худшие, то есть точки более низкого уровня. Если на основе какого-либо критерия получается кривая предпочтения типа штриховой (рис. 4.2), то мы называем такую кривую вогнутой, подразумевая под этим, что в соответствующих ей областях неопределенности имеется меньшее число лучших точек, чем при нейтральном критерии (4.5). Отметим, что такая вогнутая кривая предпочтения характеризует пессимистическую исходную позицию. Кривые предпочтения типа сплошной на рис. 4.2 соответствуют оптимистическому подходу, поскольку на этот раз в сравнении с нейтральным критерием больше точек из областей неопределенности принадлежит к числу лучших; мы называем такие кривые выпуклыми. Предельный случай пессимистического подхода образуют, очевидно, граничные прямые квадранта I, а оптимистического—граничные прямые квадранта III, и чем ближе подходит кривая предпочтения к этим граничным прямым, тем в большей степени соответствующий критерий представляет пессимистическую или, соответственно, оптимистическую точку зрения. Если выбор оценочной функции отдается на усмотрение лица, принимающего решение, то, как показывают табл. 4.3 и рис. 4.2, приходится считаться с возможностью различных результатов для одного и того же решения. Таким образом, принятие решения не есть чисто рациональный процесс. Опасность возникает в тех случаях, когда оценочные функции выбираются интуитивно, иногда даже без выяснения исходной позиции принимающего решение.
Всякое техническое или экономическое решение в условиях неполной информации – сознательно или неосознанно – принимается в соответствии с какой-либо оценочной функцией описанного выше типа. Как только это бывает признано явно, следствия соответствующих решений становятся лучше обозримыми, что позволяет улучшить их качество. При этом выбор оценочных функций всегда должен осуществляться с учетом количественных характеристик ситуации, в которой принимаются решения.
Таблица 4.4.
(m´2)-матрица решений
 F
E
| F 1 | F 2 |
| E 1 | E 11 | E 12 |
| E 2 | E 21 | E 22 |
| E 3 | E 31 | E 32 |
| . . . | . . . | . . . |
| Ei | ei 1 | ei 2 |
| . . . | . . . | . . . |
| Em | em 1 | em 2 |
Таблица 2.5.
Фатальная ситуация в принятии решений
| F 1 | F 2 | F 3 | … | Fj | … | Fn | |
| E 1 | E 11 | E 12 | E 13 | … | e 1 j | … | e 1 n |
