Принятие решения представляет собой выбор одного из некоторого множества рассматриваемых вариантов:  . В дальнейшем мы будем изучать наиболее часто встречающийся на практике случаи когда имеется лишь конечное, число вариантов
. В дальнейшем мы будем изучать наиболее часто встречающийся на практике случаи когда имеется лишь конечное, число вариантов 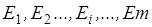 , причем обычно небольшое, хотя принципиально мыслимо и бесконечное множество вариантов
, причем обычно небольшое, хотя принципиально мыслимо и бесконечное множество вариантов  При необходимости наше рассмотрение без труда переносится на этот наиболее общий случай.
При необходимости наше рассмотрение без труда переносится на этот наиболее общий случай.
Условимся прежде всего, что каждым вариантом Ei однозначно определяется некоторый результат еi. Эти результаты должны допускать количественную оценку, и мы будем для простоты отождествлять эти оценки с соответствующими результатами, обозначая их одним и тем же символом еi.
Мы ищем вариант с наибольшим значением результата, то есть целью нашего выбора является  . При этом мы считаем, что оценки еi характеризуют такие величины, как, например, выигрыш, полезность или надежность. Противоположную ситуацию с оценкой затрат или потерь можно исследовать точно так же путем минимизации оценки или, как это делается чаще, с помощью рассмотрения отрицательных величин полезности.
. При этом мы считаем, что оценки еi характеризуют такие величины, как, например, выигрыш, полезность или надежность. Противоположную ситуацию с оценкой затрат или потерь можно исследовать точно так же путем минимизации оценки или, как это делается чаще, с помощью рассмотрения отрицательных величин полезности.
Таким образом, выбор оптимального варианта производится с помощью критерия
 (4.1)
(4.1)
Это правило выбора читается следующим образом: множество E 0 оптимальных вариантов состоит из тех вариантов Ei 0, которые принадлежат множеству Е всех вариантов и оценка еi 0которых максимальна среди всех оценок еi (логический знак /\ читается как «и» и требует, чтобы оба связываемых им утверждения были истинны).
Выбор оптимального варианта в соответствии с критерием (4.1) не является, вообще говоря, однозначным, поскольку максимальный результат  может достигаться в множестве всех результатов многократно. Необходимость выбирать одно из нескольких одинаково хороших решений на практике обычно не создает дополнительных трудностей. Поэтому в дальнейшем мы лишь упоминаем об этой возможности, не занимаясь ею более подробно.
может достигаться в множестве всех результатов многократно. Необходимость выбирать одно из нескольких одинаково хороших решений на практике обычно не создает дополнительных трудностей. Поэтому в дальнейшем мы лишь упоминаем об этой возможности, не занимаясь ею более подробно.
Только что рассмотренный случай принятия решений, при котором каждому варианту решения соответствует единственное внешнее состояние (и тем самым однозначно определяется единственный результат) и который мы называем случаем детерминированных решений, с точки зрения его практических применений является простейшим и весьма частным. Разумеется, такие элементарные структуры лежат в основании реальных процедур принятия решений. В более сложных структурах каждому допустимому варианту решения Еi вследствие различных внешних условий могут соответствовать различные внешние условия (состояния) F, и результаты еij решений. Следующий пример иллюстрирует это положение.
Пусть из некоторого материала требуется изготовить изделие, долговечность которого при допустимых затратах невозможно определить. Нагрузки считаются известными. Требуется решить, какие размеры должно иметь изделие из данного материала.
Варианты решений таковы:
Е 1 – выбор размеров из соображений максимальной долговечности, т. е. изготовление изделия с минимальными затратами в предположении, что материал будет сохранять свои характеристики в течение длительного времени;
Еm – выбор размеров в предположении минимальной долговечности;
Еi – промежуточные решения.
Условия, требующие рассмотрения, таковы:
F 1 – условия, обеспечивающие максимальную долговечность;
Fn– условия, обеспечивающие минимальную долговечность;
Fj – промежуточные условия.
Под результатом решения еij здесь можно понимать оценку, соответствующую варианту Еi и условиям Fj и характеризующую экономический эффект (прибыль), полезность или надежность изделия. Мы будем называть такой результат полезностью решения.
Семейство решений описывается некоторой матрицей (табл. 4.1). Увеличение объема семейства по сравнению с рассмотренной выше ситуацией детерминированных решений связано как с недостатком информации, так и с многообразием технических возможностей.
Конструктор и в этом случае старается выбрать решение с наилучшим результатом, но, так как ему неизвестно, с какими
Основная формальная структура принятия решений
Таблица 4.1.
Матрица решений || eij ||
| F 1 | F 2 | F 3 | … | Fj | … | Fn | |
| E 1 | e 11 | e 12 | e 13 | … | e 1 j | … | e 1 n |
| E 2 | e 21 | e 22 | e 23 | … | e 2 j | … | e 2 n |
| E 3 | e 31 | e 32 | e 33 | … | e 3 j | … | e 3 n |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| Ej | ej 1 | ej 2 | ej 3 | … | eij | … | emn |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
| Em | Em 1 | em 2 | em 3 | … | emj | … | emn |
условиями он столкнется, он вынужден принимать во внимание все оценки eij, соответствующие варианту Еi. Первоначальная задача максимизации  согласно критерию (4.1) должна быть теперь заменена другой, подходящим образом учитывающей все последствия любого из вариантов решения Ei.
согласно критерию (4.1) должна быть теперь заменена другой, подходящим образом учитывающей все последствия любого из вариантов решения Ei.






