Из требований, предъявляемых рассмотренными критериями к анализируемой ситуации, становится ясно, что вследствие их жестких исходных позиций они применимы только для идеализированных практических решений. В случаях, когда требуется слишком сильная идеализация, можно одновременно применять поочередно различные критерии. После этого среди нескольких вариантов, отобранных таким образом в качестве оптимальных, приходится все-таки волевым образом выделять некоторое окончательное решение. Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора.
Выбор решения по классическим критериям проиллюстрируем следующим примером.
Пусть некоторую машину (технологическую установку, конвейер, станок и тому подобные) требуется подвергнуть проверке с приостановкой, естественно, ее эксплуатации. Из-за этого приостанавливается выпуск продукции. Если же эксплуатации машины помешает не обнаруженная своевременно неисправность, то это приведет не только к приостановке работы, но и дополнительно к поломке.
Варианты решения таковы:
E 1 – полная проверка;
Е 2 – минимальная проверка;
Е 3 – отказ от проверки.
Машина может находиться в следующих состояниях:
F 1 – неисправностей нет;
F 2 – имеется незначительная неисправность;
F 3 – имеется серьезная неисправность.
Результаты включают затраты на проверки и устранение неисправности, а также затраты, связанные с потерями в продукции и с поломкой. Они приведены в таблице 4.7.
Таблица 4.7
Варианты решения о проверках машины и их оценки (в 103)
согласно ММ- и BL-критериям для qi = 0,33
| F 1 | F 2 | F 3 | ММ-критерий | BL- критерий | |||
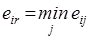
| 
| 
| 
| ||||
| E 1 | –20,0 | –22,0 | –25,0 | –25,0 | –25,0 | –22,33 | |
| Е 2 | –14,0 | –23,0 | –31,0 | –31,0 | –22,67 | ||
| Е 3 | –24,0 | –40,0 | –40,0 | –21,33 | –21,33 |
Согласно ММ-критерию (4.103.3), следует проводить полную проверку (E0={ Е 1}). BL-критерий в предположении, что все состояния машины равновероятны (qi = 0,33), рекомендует отказаться от проверки (E0={ Е 1}). Табл. 4.8 иллюстрирует применение S-критерия. Им в качестве оптимальной рекомендуется минимальная проверка.
Наш пример сознательно выбран так, что каждый критерий предлагает новое решение. Неопределенность состояния, в котором проверка застает машину, превращается теперь в отсутствие ясности, какому же критерию следовать. Таким образом, мы вроде бы мало что выиграли. Самое большее, можно было бы проверить после этого, не принимают ли величины eir для какого-нибудь критерия приблизительно |равные значения, как, например, e 2 r = 14,0·103 и e 3 r = 15,0·103 в табл. 4.8;
Таблица 4.8
Матрица остатков для примера «Решения о проверках машины»
и их оценка (в103) согласно S-критерию
| F 1 | F 2 | F 3 | S-критерий | ||

| 
| ||||
| E 1 | +20,0 | +20,0 | |||
| Е 2 | +14,0 | +1,0 | +6,0 | +14,0 | +14,0 |
| Е 3 | +2,0 | +15,0 | +15,0 |
рекомендации такого критерия выглядят менее убедительными. Поскольку различные критерии связаны с различными же аспектами ситуации, в которой принимается решение, лучше всего для сравнительной оценки рекомендаций тех или иных критериев получить дополнительную информацию о самой ситуации. Если принимаемое решение относится к сотням машин с одинаковыми параметрами, то целесообразно придерживаться BL-критерия. Если же число реализации невелико, то больший вес приобретают более осторожные рекомендации S- или ММ-критериев.
В области технических задач различные критерии часто приводят к одному результату. Предположим, что в рассматриваемом примере серьезная неисправность (состояние F 3 ) встречается вдвое чаще, чем любое другое состояние (q 1 = q 2; q 3 = 0,5); тогда ВL-критерий, как и ММ-критерий, рекомендует полную проверку (Eo ={ E 1}).
Бывают и такие ситуации, когда все критерии дают одинаковые результаты. Если для нашего примера (табл. 4.7) с помощью соответствующих мероприятий удастся так снизить затраты на полную проверку, что в соответствующей строке мы будем иметь е 11=18,0.103, e 12= –20,0·103 и e 13=22,0·103, то все три применявшихся критерия предпишут полную проверку.
Всякий вариант, избираемый в данном случае всеми рассмотренными критериями, является слабо доминирующим. Сильное доминирование имеет место, когда для всех результатов е 11 одного из рассматриваемых вариантов справедливо
e 1 j £ eij для j =1,.... п
и
e 1 j < e ij хотя бы для одного j.
Над указанным вариантом Е 1 остальные варианты доминируют. Его можно исключить из матрицы решений, так как для всякого Fj он дает худший результат, чем другие.
Если какой-либо вариант Е 1 доминирует сильно, то есть выполняются условия
e 1 j ³ eij для всех j =1,.... п и
e 1 j > eij хотя бы для одного j,
то даже при отсутствии информации о возможных внешних состояниях Fj никакой проблемы относительно принимаемого решения нет. Для всякого Fj вариант Е 1 – наилучший.






