Для определения прогибов и углов поворота произвольного сечения балки необходимо последовательно дважды интегрировать дифференциальное уравнение (11.27) в пределах каждого участка балки, затем найти постоянные интегрирования, составить уравнения прогибов и углов поворота на каждом участке и использовать эти уравнения для построения эпюр прогибов и углов поворота.
Такой метод называется методом непосредственного интегрирования дифференциального уравнения упругой линии.
Рассмотрим балку на двух шарнирных опорах, нагруженную сосредоточенной силой F (рис.11.21). Определим реакции опор и составим уравнение изгибающих моментов для каждого из двух участков, принимая начало координат на левом конце балки.
Рис.11.21
Реакции опор балки легко определяются из условий её равновесия относительно опорных точек. Величины реакций для заданной балки были вычислены ранее и приведены на рисунке 11.21.
Составляем уравнения изгибающих моментов на участках 1 и 2 балки.
Участок 1(BD) (0 £ х £ b)
Участок 2(D С) (b £ х £ 
)
Составляем дифференциальные уравнения упругой линии (изогнутой оси балки) для каждого участка:
Участок 1(BD) (0 £ х £ b)
(11.28)
Участок 2(DС) (b £ х £ )
(11.29)
Интегрируем уравнения (11.28) и (11.29) первый раз и получаем уравнение углов поворота поперечных сечений балки:
(11.30)
(11.31)
Интегрируем уравнения (11.28) и (11.29) второй раз, или уравнения (11.30) и (11.31) первый раз и получаем уравнение прогибов балки:
(11.32)
(11.33)
При интегрировании дифференциальных уравнений используем прием Клебша, то есть выражение (x-b)dx заменяем выражением (x-b)d(x-b) и интегрирование выполняем без раскрытия скобок.
Уравнение (11.30), (11.31), (11.32) и (11.33) содержат четыре неизвестные постоянные интегрирования: С1, С2, D1 и D2.
Для определения этих постоянных используем следующие четыре условия: прогибы оси балки на опорах равняются нулю (то есть при x=0 и x = имеем 
и 
), прогибы и углы поворота на стыке двух участков имеют одинаковые величины (то есть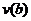 
для левого участка BD равняется 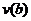для правого участка DС, аналогично 
для левого участка BD равняется для правого участка DС).
Подставим в уравнение (11.32) вместо x его значение x=0, а в уравнение (11.33) вместо x его значение x= , тогда получим:
D1=0 и 
(11.34)
Подставим в уравнение (11.32) и (11.33) вместо x его значение x= b и приравняем правые части этих зависимостей, в результате получим:
(11.35)
Подставим в уравнение (11.30) и (11.31) вместо x его значение x= b и приравняем правые части этих зависимостей, в результате получим:
, откуда находим С1 = С2, тогда из равенства (11.35) имеем D2 = 0, а из равенства (11.34) находим
С1 = С2 = 
Теперь заменим в уравнениях (11.30) - (11.33) постоянные интегрирования найденными их величинами, в результате получим окончательные уравнения прогибов и углов поворота для каждого участка балки:
Участок 1(BD) (0 £ х £ b)
(11.36)
(11.37)
Участок 2(СD) (b £ х £ )
(11.38)
(11.39)
Используя последние четыре уравнения, легко определить величины прогибов и углов поворота произвольного сечения балки, а также определить максимальный прогиб балки в сечении, угол поворота которого равняется нулю.
Поперечное сечение балки, которое получает максимальное прогиб, находится на расстоянии x1 от левой опоры балки. Это расстояние легко установить из условия равенства нулю угла поворота. Приравняем к нулю правую часть уравнения (11.36), получим:
, откуда находим:
Рассмотрим случай, когда сила F приложена посредине пролета балки. В этом случае b = c = /2, тогда:
С1 = С2 = 
и уравнения прогибов и углов поворота упрощаются и проводятся к следующему виду:
Участок 1(BD) (0 £ х £ /2)
(11.40)
(11.41)
Участок 2(СD) ( /2 £ х £ )
(11.42)
(11.43)
Определим, например, прогиб и угол поворота посредине пролета балки, то есть при x = /2. Из уравнений (11.40) и (11.41) находим: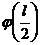 
= 0, и 
Отрицательный знак прогиба означает, что прогиб балки направлен вниз от её оси.
