Если в каком-либо поперечном сечении балки возникают изгибающий момент М y и поперечная сила Qz, то деформация балки имеет название прямого поперечного изгиба. Напряжения, которые возникают в произвольной точке поперечного сечения, определяются отдельно от действия изгибистого момента М y и поперечной силы Qz.
От действия изгибающего момента возникают нормальные напряжения, которые определяются таким же образом, как и при чистом изгибе, то есть с использованием формул (11.19) и (11.20).
От действия поперечной силы возникают касательные напряжения τ z, которые определяются с использованием формулы Журавского.
Приводим эту формулу без доказательства:
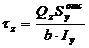(11.21)
где Qz – поперечная сила в поперечном сечении балки,
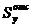– статический момент относительно оси у той части площади сечения, которая лежит выше или ниже от точки, где определяется напряжение (эта часть площади называется отсеченной),
b – ширина поперечного разреза балки в точке, где определяется напряжение,
I y – момент инерции поперечного сечения балки относительно оси y.
Рассмотрим поперечное сечение балки прямоугольной формы, размеры сторон которого равняются b и h (рис. 11.17,а) и построим эпюру касательных напряжений по высоте этого сечения.
Определим касательное напряжение в точке C сечения, которая расположена на расстоянии z от горизонтальной центральной оси y. Проведем через точку C прямую линию 1-1, параллельную оси y и определим статический момент относительно оси у той части площади, которая расположена выше прямой 1-1 (эта площадь заштрихована на рис.11.17,а).
Рис. 11.17
Учитывая, что момент инерции прямоугольного сечения относительно горизонтальной оси y равняется:
, получим по формуле (11.21):
Анализируя полученную зависимость между касательным напряжением и размерами поперечного сечения балки, легко заметить, что касательные напряжения изменяются по высоте прямоугольника согласно уравнению квадратичной параболы. Если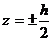 
, то τ z = 0, а если z = 0, то касательные напряжения принимают максимальные значения, которые равняются 
, где А – площадь поперечного сечения балки. На рис.(11.17,б) построена эпюра касательных напряжений для прямоугольного сечения балки.
Рассмотрим поперечное сечение балки в виде двутавра, составленного из вертикального прямоугольника, который называется стенкой и имеет очень малую ширину по сравнению с высотой и двух горизонтально расположенных прямоугольников, которые имеют название верхней и нижней полок этого двутавра (рис.11.18,а). Полки имеют ширину сечения, значительно превышающую их высоту.
Особенность такого сечения заключается в том, что переход от стенки к полки характеризуется резким изменением его ширины и сопровождается резким изменением касательного напряжения. Обозначим цифрами 1,2,3,0 характерные точки двутавра по высоте верхней части относительно оси y и определим касательные напряжения в этих точках по формуле Журавского.
Напряжение τ1 = 0 потому, что эта точка является верхней точкой сечения. Для определения напряжений в точках 2 и 3 необходимо вычислить статический момент верхней полки относительно оси y, то есть 
и подставить это значение в числитель формулы (11.21), а в знаменатель (кроме значения момента инерции Iy) подставить значение ширины сечения в точке, где определяется напряжение. Для точки 2 мы должны подставить величину b, а для точки 3 величину d. В результате будем иметь:
Учитывая, что d << b, получим: τ2 <<τ3.
Максимальное значение касательного напряжения возникает в точке 0 на оси y, то есть в точке нейтральной линии. Оно определяется следующей формулой:
На рис.11.18,б приведена эпюра касательных напряжений по высоте сечения двутавровой формы.
Касательные напряжения в точках полок двутавра очень малы по сравнению с касательными напряжениями, которые возникают в точках стенки, поэтому их не учитывают и епюру касательных напряжений строят только для стенки (рис.11.18,в).
Рис. 11.18
