Нормальные напряжения в поперечных разрезах

Балки при чистом изгибе

 

Чистый изгиб балки возникает в случае, когда она нагружена в одной из главных плоскостей инерции сосредоточенными моментами. На рис.11.14 приведено пример чистого изгиба балки, который возникает при ее нагружении сосредоточенным моментом. В этом случае реакция правой опоры равняется по модулю действующему моменту и имеет противоположное направление. Эпюра изгибающих моментов очерчена прямой, параллельной оси балки, то есть во всех поперечных сечениях балки изгибающий момент имеет одинаковую величину , а поперечная сила равняется нулю.

 Для определения напряжений рассмотрим три аспекта этой задачи: статический, геометрический и физический

                                                                           

                                             Рис. 11.14

                                                                      

Статический аспект чистого изгиба. Если с помощью двух поперечных сечений, расстояние между которыми есть бесконечно малая величина dх, выделить элемент балки, то он будет находиться в равновесии под действием изгибающих моментов  (рис.11.15,а).

             

                                            Рис. 11.15

 

Допустим, что поперечное сечение балки имеет прямоугольную форму и произвольные размеры (рис. 11.15,б). Проведем главные оси инерции y и z и выделим элементарную часть dA этой площади сечения вокруг точки с координатами (у, z). От действия изгибающего момента в плоскости правого сечения возникают нормальные напряжения , которые распределены по всей его площади. На элементарную часть площади dA с положительными координатами (у, z) правого сечения действует равнодействующая внутренних усилий, которая направлена параллельно осе х  и равняется произведению σdA. Усилия σdA параллельны оси х и составляют пространственную систему параллельных сил. Поэтому, для равновесия элемента балки длиной dх нужно выполнить три условия равновесия:

               ; ; .

Используя эти условия, получаем следующие уравнения равновесия.

                                                                                                                (11.10)

                                                                                                        (11.11)

                                                                                                              (11.12)

Поскольку закон распределения напряжений по площади поперечного сечения балки неизвестен, то из этих уравнений пока еще не возможно определить напряжения. Для этого нужно дополнительно рассмотреть геометрический, а затем физический аспекты задачи.

Рассмотрим деформации, которые получат волокна элемента балки длиной dх после изгиба (рис. 11.16).

От действия внешних моментов балка изгибается, т.е. её волокна принимают криволинейную форму. Верхние волокна удлиняются, а нижние укорачиваются. Таким образом, между этими слоями волокон существует такой слой волокон, длина которых остается неизменной. Этот слой имеет название нейтрального слоя. При этом поперечные сечения остаются плоскими, согласно гипотезе плоских сечений.

В реальных условиях загружения балки деформации изгиба имеют очень малые величины. Поэтому можно пренебречь искривлениями волокон элемента балки бесконечно малой длины и считать их прямолинейными. Закрепим условно левое сечение рассматриваемого элемента, тогда правое его сечение получит поворот на элементарный угол dφ и плоскости граничных сечений пересекутся по прямой, следом которой на плоскости рисунка является точка О.

                                 

 

                                           Рис.11.16

 

Обозначим волокно нейтрального слоя через mn = dх, а его расстояние от точки О, где пересекаются плоскости сечений, через r. Тогда из треугольника mnО найдем:

                                         mn = dх = r dφ

Рассмотрим волокно на расстоянии z от нейтрального слоя и найдем его длину ef′ после изгиба балки    ef′ = ( r + z) dφ.

Абсолютная деформация этого волокна будет равняться:

 

               D _ef = ef′ - mn = ( r + z)dφ - r dφ = z dφ

 

Найдем относительную деформацию этого волокна:

 

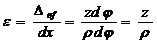           , то есть                                            (11.13)

Величина r имеет название радиуса кривизны нейтрального слоя, а отношение 1/r является кривизной этого слоя волокон.

Таким образом, относительная деформация какого-либо волокна прямо пропорциональна расстоянию этого волокна от нейтрального слоя и обратно пропорциональна радиусу кривизны нейтрального слоя.                                             

Физический аспект задачи. Он заключается в том, что деформация балки происходит в пределах упругости материала, когда напряжения пропорциональные относительным деформациям, то есть

        или 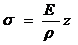                                                        (11.14)

Подставим в уравнение (11.10) – (11.12) вместо s его значение согласно зависимости (11.14), в результате получим:

 

                                                                                                              (11.15)             

                                                                                                 (11.16)                                                         

                                                                                                                  (11.17)   

 

Интеграл зависимости (11.15) является статическим моментом Sy площади поперечного сечения балки относительно оси y. Учитывая, что Е/r ¹ 0, имеем S _y = 0, то есть ось у проходит через центр тяжести площади сечения.

Интеграл зависимости (11.17) является центробежным моментом инерции (I _yz) площади поперечного сечения относительно осей y и z. Так как он равняется нулю, то оси y и z является главными осями инерции площади поперечного сечения балки, то есть, хотя бы одна из этих осей является осью симметрии сечения.

Наконец интеграл зависимости (11.16) является моментом инерции (I _y) относительно оси y, тогда из указанной зависимости получаем:

                                                                                                           (11.18)

Таким образом, нейтральный слой волокон лежит в плоскости xОy (горизонтальной плоскости, которая проходит через ось балки), а нейтральная линия совпадает с осью y. Во всех точках этой линии напряжения равняются нулю, а кривизна изогнутой оси балки пропорциональна изгибающему моменту и обратно пропорциональна жесткости поперечного сечения при изгибе, то есть величине ЕI _y.

Найдем 1/r из зависимости (11.14)     и подставим это значение в формулу (11.18). В результате получим:

                , откуда                                               (11.19)

Таким образом, при М _y > 0, напряжения в точках сечения с положительной координатой z будут отрицательными (напряжениями сжатия), а в точках сечения с отрицательной координатой z будут положительными (напряжениями растяжения).

При определении нормальных напряжений за формулой (11.19) необходимо учитывать знаки изгибающего момента и координаты z точки сечения, в котором определяется напряжение. В этом случае получим напряжение с действительным знаком.

На рис. 11.15,в показана епюра  s в поперечном сечении прямоугольной формы при чистом изгибе балки (при М _y< 0). Справа от нулевой линии отложены напряжения растяжения, а слева - напряжение сжатия. По ширине поперечного сечения балки нормальные напряжения не изменяются.

По пюре напряжений легко установить, что максимальные напряжения возникают в точках сечения, которые наиболее удалены от нейтральной оси y, то есть при z = z_max. Подставим эту величину в формулу (11.19), тогда отношение момента инерции поперечного сечения балки к z_max  будет равна моменту сопротивления площади сечения относительно оси y, т.е. .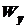

В результате получим:

          ; или                                             (11.20)

При использовании формул (11.20) необходимо помнить, что при изгибающем моменте, имеющим знак плюс, растягивающие напряжения возникают в нижних волокнах балки, а при изгибающем моменте, имеющим знак минус, растягивающие напряжения возникают в верхних волокнах балки.