Определение перемещений в балках, или стержневых системах, состоящих из нескольких стержней постоянной жесткости, можно значительно упростить путем применения специального способа определения интегралов (11.58) или (11.59).
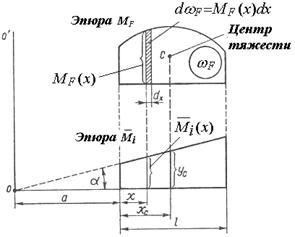
Рис.11.26
Рассмотрим один участок балки в действительном и возможном состояниях и допустим, что на этом участке, длина которого равняется 
, известны уравнения изгибающих моментов и построены их эпюры (рис.11.26). Эпюра изгибающих моментов в действительном состоянии может иметь криволинейную форму, а эпюра
изгибающих моментов в возможном (единичном) состоянии всегда ограничена прямой линией, т.е. прямолинейна. Определим для этого участка интеграл:
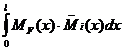11.60)
В этом интеграле 
- есть ордината эпюры изгибающих моментов действительного состояния на расстоянии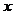 
от начала участка, а 
- есть ордината эпюры изгибающих моментов возможного состояния на том же расстоянии.
Из рисунка 11.26 следует, что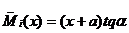 
. Подставим это значение в интеграл (11.60), получим:
= 
= 
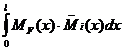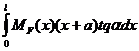(11.61)
Произведение 
- равняется площади элементарного прямоугольника эпюры , которая заштрихована на рис.11.26, то есть 
. С учетом этого выражения интеграл (11.60) преобразуется к виду:
= 
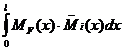(11.62)
Интеграл правой части зависимости (11.62) является статическим моментом площади эпюры относительно вертикальной оси ОО′.
Из теоретической механики известно, что этот статический момент равняется произведению площади эпюры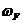 
на расстояние от оси ОО′ до центра тяжести эпюры, то есть на расстояние 
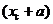. Тогда получим:
== 
,
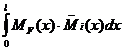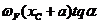Учитывая, что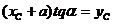 
, найдем:
== 
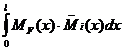(11.63)
Заменим интеграл формулы Мора-Максвелла (11.58) его значением согласно зависимости (11.63) получим окончательно:
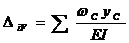(11.64)
Таким образом, перемещение (прогиб или угол поворота) какого-либо сечения балки равняется сумме произведений площадей эпюры изгибающих моментов в заданном состоянии на ординаты эпюры изгибающих моментов в возможном состоянии, взятые под центрами тяжести указанных площадей, разделенных на жесткость балки.
Определение перемещений с использованием формулы (11.64) называется правилом перемножения эпюр изгибающих моментов в двух состояниях (действительном в возможном).
Это правило было предложено в 1925 году студентом Московского института железнодорожного транспорта А.К.Верещагиным и носит его имя.
Для определения перемещений по этому правилу нужно:
1) Построить грузовую эпюру М F в заданном состоянии балки;
2) Образовать возможное состояние балки путем загружения её силой
F i=1, или моментом М i=1 и построить единичную эпюру изгибающих
моментов;
3) Разделить две построенные эпюры изгибающих моментов на участки так, чтобы на каждом из них хотя бы одна из эпюр была прямолинейной;
4) Определить площади и положения центров тяжести эпюры изгибающих моментов заданного состояния на каждом участке, а также ординаты эпюры изгибающих возможного состояния под центрами тяжести первой эпюры;
5) Перемножить на каждом участке площади одной эпюры на ординаты другой эпюры. Полученные произведения разделить на жесткости участков балки и найти их сумму (формула 11.64).
