Изгибе балки
Возле некоторой точки балки выделим элементарный параллелепипед 1-2-3-4 (рис.11.19,а), две грани которого расположены в поперечных сечениях балки (грани 1-2 и 3-4), а две другие грани параллельные нейтральному слою (грани 1-4 и 2-3).
Рис. 11.19
Высота параллелепипеда равняется ширине поперечного сечения балки и расположена перпендикулярно к плоскости рисунка. На гранях параллелепипеда действуют нормальные напряжения σ и касательные напряжения τ. На рис.11.19,б показаны эти напряжения, направления которых отвечают положительным знакам изгибающего момента и поперечной силы в поперечных сечениях балки. Передняя и задняя грани элементарного параллелепипеда совпадают с боковыми поверхностями балки, на которых отсутствующие нагрузки. Поэтому на этих гранях не возникают ни нормальные, ни касательные напряжения.
Если повернуть элементарный параллелепипед на некоторый угол, то напряжения на его гранях изменятся. На каждой из них будут действовать нормальные и касательные напряжения. Но существуют и такие грани (плоскости), на которых действуют только нормальные, или только касательные напряжения. Плоскости балки, в которых действуют только нормальные напряжения, называют главными плоскостями, а напряжения называют главными нормальными напряжениями. Эти напряжения имеют соответственно наибольшее и наименьшее значение σ max и σ min. В случае прямого поперечного изгиба балки эти напряжения определяются по формулам, которые приводим без доведения:
и 
(11.22)
Существуют также взаимно перпендикулярные плоскости, на которых нормальные напряжения равняются нулю. Эти плоскости называют плоскостями сдвига. На них действуют максимальные и минимальные касательные напряжения, которые определяются по формулам:
, 
11.23)
Расчет балки на прочность
Расчет балки на прочность при поперечном изгибе осуществляется в зависимости от максимального нормального напряжения, которое возникает в опасном сечении балки. Опасным сечением балки называется сечение, в котором действует максимальный по модулю изгибистый момент M y = M max.
Поэтому максимальные напряжения в опасном сечении балки определяются по формуле (11.20).
Максимальные напряжения не должны превышать расчетного сопротивления материала балки при изгибе, то есть:
(11.24)
Условие (11.24) называется условием прочности балки при изгибе. Используя это условие, можно выполнить три вида расчета балки при изгибе:
1) Сравнить рабочие напряжения в опасном сечении балки с расчетным сопротивлением. Если известен максимальный изгибающий момент в опасном сечении, и размеры сечения балки, то по формуле (11.20) можно определить напряжения и сравнить их с расчетным сопротивлением, т.е. убедиться в том, что условие (11.24) выполняется. Такой расчет называется проверочным.
2) Подобрать размеры поперечного сечения балки, которые удовлетворяют условию прочности. Для этого необходимо определить из условия (11.24) требуемую величину момента сопротивления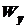 
сечения балки и найти его размеры при заданной форме. Если поперечное сечение балки имеет форму прокатного двутавра, то номер двутавра находим из таблиц сортамента прокатной стали. Момент сопротивления этого двутавра должен иметь значение, близкое к вычисленному значению. При этом рабочее напряжение не должно превышать расчетного сопротивления больше чем на 5%. Этот расчет называется проектным. Он является основным видом расчетов на прочность.
3) Определить допустимую нагрузку на балку. В этом случае известны размеры поперечного сечения балки и расчетное сопротивление. Тогда из условия (11.24) определяется допустимое значение изгибающего момента и находим допустимую нагрузку.
Методика решения этих задач разная для балок, изготовленных из пластичных и хрупких материалов потому, что для пластичных материалов расчетное сопротивление при растяжении и сжатии имеет одинаковую величину, а для хрупких материалов расчетное сопротивление при растяжении значительно меньше расчетного сопротивления при сжатии.
Для балок из пластичных материалов целесообразно принимать симметричные формы поперечных сечений относительно оси y (например, двутавровое сечение), а для балок из хрупких материалов не симметричные (например, сечение в виде тавра, составленное из двух уголков). В первом случае максимальные напряжения растяжения и сжатия будут иметь одинаковые значения, а во втором случае эти напряжения будут разными. При расчете балок из хрупких материалов необходимо расположить сечение так, чтобы максимальное напряжение сжатия было больше максимального напряжения растяжения.
