Моментов
Как известно эпюра некоторого усилия это есть график, который характеризует изменение данного усилия вдоль оси балки.
Построить эпюры поперечных сил Q z(x) и изгибающих моментов M y(x) для статически определимой балки можно с использованием классического метода сечений, или с использованием практического метода площадей.
Рассмотрим последовательно эти два метода.
Метод сечений. Для построения епюр поперечных сил и изгибистых моментов этим методом необходимо:
1) Определить реакции опор балки, используя условия её равновесия (для балки-консоли, которая имеет одну жесткую опору можно не определять реакции опор, а рассматривать ее от свободного конца);
2) Разделить балку на участки, которые ограничены точками, где приложены сосредоточенные силы или моменты и границами распределенных нагрузок;
3) Выбрать произвольные сечения на каждом участке и обозначить их расстояния от начала координат через x1, x2, x3 и т.д. Эти расстояния изменяются в пределах значений, которые легко определить для каждого участка. Если балка имеет многих участков, то для упрощения уравнений и ускорения расчета начало координат для части участков целесообразно принять в левой крайней точке оси балки и ось x направить вправо, а для другой части участков начало координат принять в правой крайней точке оси балки и ось x направить влево.
4) Составить уравнения поперечных сил и изгибающих моментов, используя их определения и правила знаков;
5) Исследовать эти уравнения и определить величины поперечных сил и изгибающих моментов в характерных сечениях балки. При линейных уравнениях усилий достаточно вычислить их значения в начале и в конце участка. Если уравнения усилий являются квадратичными или более высокого порядка, то необходимо вычислить как минимум три значения (на концах участка и посредине);
6) Выбрать подходящий масштаб и отложить от прямых линий, проведенных параллельно оси балки, ординаты, равные найденным значениям усилий в соответствующих сечениях. При этом, положительные ординаты эпюры поперечных сил откладывают вверх, а отрицательные – вниз от нулевой прямой. Положительные ординаты эпюры изгибающих моментов откладывают вниз от нулевой прямой, а отрицательные – вверх. На каждом участке балки соединяют вершины ординат прямыми или кривыми линиями, в зависимости от характера их уравнений.
Пример 11.1. Построить эпюры поперечных сил Q z(x) и изгибающих моментов M y(x) для балки-консоли нагруженной силой F на правом конце и жестко закрепленной на левом конце (рис.11.8,а), если длина балки равняется  м.
м.
Выполняем решение задачи в следующей последовательности:
1) Реакции опоры В не определяем, потому что усилие в произвольном поперечном сечении балки можно определить из условия равновесия правой части балки относительно этого сечения;
2) Рассматриваем один участок заданной балки;
3) Проводим поперечное сечение 1-1 на переменном расстоянии x от свободного конца балки и находим интервал изменения величины x (0 £ х £  );
);
4) Составляем уравнение усилий Q z(x) и M y(x), пользуясь их определениями и правилами знаков:

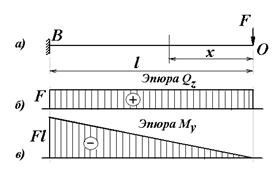
Рис. 11.8
Анализируем эти уравнения. Поперечная сила Q z(x) не зависит от х, то есть является постоянной величиной положительного знака для всех сечений балки, а изгибающий момент M y(x) линейно зависит от абсциссы x и его ординаты имеют отрицательный знак.
5) Определяем значение M y(x) в двух сечениях балки:
при х = 0 - M y(0) = 0, при х =  м -M y(l) = - F
м -M y(l) = - F  .
.
6) Строим эпюры. Сначала проводим нулевую линию эпюры Q z(x) параллельно оси балки и откладываем вверх от нее положительное значение поперечной силы, то есть величину F, и проводим прямую параллельную нулевой линии. Получаем эпюру Q, которая имеет форму прямоугольника. Потом проводим нулевую линию эпюры M y(x) и откладываем вниз от нее вычисленные величины изгибающего момента в начале участка и на конце балки, т.е. ординаты равные нулю и - F  , соответственно. Полученные ординаты соединяем прямой линией, наклоненной к оси балки под углом, тангенс которого равняется поперечной силе. Построенные эпюры поперечных сил и изгибающих моментов должны быть равномерно заштрихованы по длине балки прямыми линиями, перпендикулярными оси балки. Это есть ординаты этих епюр. Ордината епюри Q z(x) в произвольном сечении балки равняется поперечной силе в этом сечении. Аналогично, ордината эпюры изгибающих моментов в произвольном сечении балки равняется изгибающему моменту в этом сечении.
, соответственно. Полученные ординаты соединяем прямой линией, наклоненной к оси балки под углом, тангенс которого равняется поперечной силе. Построенные эпюры поперечных сил и изгибающих моментов должны быть равномерно заштрихованы по длине балки прямыми линиями, перпендикулярными оси балки. Это есть ординаты этих епюр. Ордината епюри Q z(x) в произвольном сечении балки равняется поперечной силе в этом сечении. Аналогично, ордината эпюры изгибающих моментов в произвольном сечении балки равняется изгибающему моменту в этом сечении.
Используя построенные эпюры, можно определить реакции защемляющей опоры В балки. Вертикальная реакция указанной опоры будет равна ординате эпюры поперечних сил, взятой под этой опорой, т.е. величине силы F. Учитывая знак эпюры поперечних сил устанавливаем, что вертикальна реакция VB будет направлена вверх.
Опорный момент защемления балки равен изгибающему моменту в опорном сечении, т.е. величине F  . Учитывая знак эпюры изгибающих моментов, устанавливаем, что опорный момент направлен против часовой стрелки.
. Учитывая знак эпюры изгибающих моментов, устанавливаем, что опорный момент направлен против часовой стрелки.
Пример 11.2. Построить эпюры Q z(x) и M y(x) для балки-консоли, размеры и нагрузки которой приведено на рис. 11.9,а
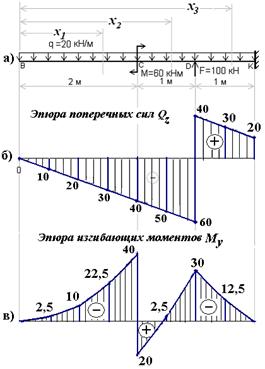
Рис.11.9
Решение задачи
1) Как и в примере 1 реакции опоры К не определяем.
2) Делим балку на три участка BС и СD и DК.
3) Выбираем произвольные сечения балки на каждом участке, которые расположены на переменных расстояниях х1, х2, х3 от начала координат (от точки В).
Составляем уравнение Q z(x) и M y(x) на каждом участке и определяем характер их изменения по длине балки и пределы их существования.
Участок BС (0 £ х1 £ 2м)

Поперечная сила линейно зависит от x1, а изгибающий момент изменяется в соответствии с уравнением квадратной параболы.При составлении этих уравнений заменяем мысленно распределенную нагрузку, которая действует слева от сечения 1-1, равнодействующей сосредоточенной силой. Эта сила равняется произведению  направлена вниз и приложена в центре тяжести прямоугольника со сторонами
направлена вниз и приложена в центре тяжести прямоугольника со сторонами  и х1, то есть на расстояниях х1/2 от свободного конца балки и от сечения 1-1.
и х1, то есть на расстояниях х1/2 от свободного конца балки и от сечения 1-1.
Участок СD (2 £ х2 £ 3м)
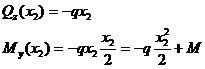
Поперечная сила на этом участке также линейно зависит от x2, а изгибающий момент изменяется по уравнению квадратной параболы, которая по отношению к квадратной параболе на участке BС имеет смещение в сторону положительных ординат на величину внешнего сосредоточенного момента M.
Участок DК (3 £ х3 £ 4м)
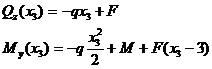
Поперечная сила на третьем участке линейно зависит от x3, а изгибающий момент изменяется по уравнению квадратичной параболы.
4) Определяем величины Q z(x) и M y(x) в характерных сечениях каждого участка балки.
Участок BС:
Находим две ординаты поперечной силы (в начале и в конце участка):
При х1 = 0: Q z(0)) = 0; при х1 = 2м: Q z(2)= -20∙2 = -40 кН
и три ординаты изгибающего момента (в начале, посередине и в конце участка):
при х1 = 0: M y(0)= 0;
при х1 = 1м: M y(1) = -20∙12/2 = -10кНм;
при х1 = 2м: M y(2)= -20∙22/2 = -40кНм.
Участок СD:
Для поперечной силы определяем два значения:
при х2 = 2м - Q z(0)) = -20∙2 = = -40кН,
при х2 = 3м - Q z(0)) = -20∙3 = - 60 кН.
Для изгибающего момента определяем три значения:
при х2 = 2м: M y(2) = -20∙22/2 + 60 = 20 кНм;
при х2 = 2,5м: M y(2,5) = -20∙2,52/2 + 60 = -2,5 кНм;
при х2 = 3м: M y(3) = -20∙32/2 +60 = -30кНм.
Участок DК:
На этом участке также определяем два значения поперечной силы и три значения изгибающего момента:
при х3 = 3м - Q z(3)= -20∙3 + 100 = 40 кН;
M y(3)= -20∙32/2 +60 = -30кНм
при х3 = 3,5м: M y(3,5)= -20∙3,52/2 +60 +100(3,5-3) = -12,5 кНм;
при х3 = 4м: - Q z(4)= -20∙4 + 100 = 20 кН, а
M y(4)= -20?42/2 + 60 +100(4-3) =0
5) Строим эпюры Q z и M y, используя полученные их значения (рис.11.9,б и в).
Ордината эпюры Q z под опорой К равняется вертикальной реакции этой опоры, то есть Vк = 20 кН. В соответствии со знаком эпюры Q z эта реакция направлена вниз. Ордината эпюры M y равняется опорному моменту Mк=0, то есть в данном случае опорный момент не возникает.
Пример 11.3. Построить епюри Q z и M y для балки на двух шарнирных опорах, нагруженной сосредоточенной силой F (рис.11.10).
Последовательность решения задачи:
1) Определяем реакции опор VВ и VС из условий равновесия балки:
ΣMВ=0 VС ·  - F∙b =0, откуда VС = F∙b / l
- F∙b =0, откуда VС = F∙b / l
ΣM С =0 - V B ·  - F∙c =0, откуда V B = F∙c / l
- F∙c =0, откуда V B = F∙c / l
2) Делим балку на два участка, расположенные слева и справа от точки приложения силы F.
3) Выбираем произвольные сечения 1-1 и 2-2 баки на переменных расстояниях x1 от опоры В и x2 от опоры С, то есть начало координат для участка BD принимаем в точке В, а начало координат для правого участка DС принимаем в точке С.
4) Составляем уравнение поперечных сил и изгибистых моментов на каждом участке балки:
Участок BD (0 £ х1 £ b)
Qz(x1)= VВ = F∙ c/ l и My(x1)= VB∙ x1 = F∙ c∙ x1/ l

Рис.11.10
Участок СD (0 £ х2 £ с)
Qz(x2)= - VC = - F∙ b/ l и My(x2)= VC∙ x2 = F∙ b∙ x2/ l
5) Определяем ординаты поперечных сил и изгибающих моментов в начале и на конце каждого участка и строим эпюры этих усилий:
Участок BD
Поперечная сила на этом участке не зависит от х1 и имеет постоянную величину в произвольном сечении. Эта величина равняется F∙ c/ l. Отложим это значение вверх от нулевой прямой и проведем прямую линию параллельно оси балки (рис.11.10,в). Изгибающий момент на этом участке линейно зависит от х1, поэтому нужно определить две ординаты эпюры (в начале и на конце участка): при х1=0 имеем My(0) = 0, а при х1=b имеем My(b) = F∙ b∙ c/ l. Отложим эту величину под силой F вниз от нулевой прямой и соединим ее с нулевой точкой под опорой В. Получим эпюру изгибающих моментов на участке BD (рис.11.10,г)
Участок СD
Поперечная сила на этом участке не зависит от х2 и имеет постоянную величину для произвольного сечения. Эта величина равняется - F∙ b/ l. Отложим это значение вниз от нулевой прямой и проведем прямую линию параллельно оси балки. В результате получим эпюру Qz на участке СD и полную эпюру для заданной балки (рис.11.10,в). Изгибающий момент на этом участке линейно зависит от х2, поэтому нужно определить две ординаты эпюры (в начале и на конце участка): при х2=0 имеем My(0) = 0, а при х2=c имеем
My(b) = F∙ b∙ c / l. Эта величина совпадает с величиной изгибающего момента на конце участка BD, то есть под силой F. Соединим ее с нулевой точкой под опорой С и получим эпюру изгибающих моментов на участке СD и полную эпюру для заданной балки (рис.11.10,г).
Проанализируем построенные эпюры с использованием дифференциальных зависимостей между внутренними усилиями и внешней нагрузкой.
1) На обоих участках балки отсутствует распределенная нагрузка, поэтому эпюра поперечных сил ограничивается прямыми линиями, параллельными оси балки, а эпюра изгибающих моментов ограничивается прямыми, наклоненными к оси балки.
2) На левом участке балки поперечная сила имеет положительный знак, поэтому изгибистый момент возрастает от нуля до максимальной величины F∙ b∙ c/ l.. На правом участке поперечная сила имеет отрицательный знак, поэтому изгибающий момент убывает от максимальной величины F∙ b∙ c/ l. до нуля. Таким образом, в сечении балки, где поперечная сила меняет знак из положительного на отрицательный, изгибающий момент достигает максимального значения.
3) Тангенсы углов наклона эпюры изгибающих моментов к оси балки равняются поперечным силам на соответствующих участках.
Пример 11.4. Для равномерно нагруженной балки на двух шарнирных опорах построить эпюры поперечных сил Qz и изгибающих моментов My (рис.11.11,а). 
Рис.11.11
Последовательность решения задачи:
1) Определяем реакции опор VА и VВ из условий равновесия балки:
ΣM В =0 V С ∙ l - q ∙ l ∙ l /2 =0, откуда V C = q l 2 /2
ΣM С =0 - V B∙ l + q ∙ l ∙ l /2 =0, откуда V B = q l 2 /2 В данном случае реакции опор можно определить с использованием симметрии нагрузки относительно опор. Если балка нагружена симметрично относительно опор, то реакции опор равняются половине равнодействующей нагрузки и направлены противоположно этой равнодействующей. Равнодействующая равномерно распределенной нагрузки равняется площади этой нагрузки, то есть произведения q∙ l. Тогда реакции опор будут равны:
VС = VВ = q∙ l/2.
2) Балка имеет один участок, ограниченный опорными реакциями.
3) Выбираем произвольное сечение 1-1 баки на переменном расстоянии x от опоры B, то есть от начала координат, принятому в точке B.
4) Составляем уравнение поперечных сил и изгибающих моментов на этом участке балки:
Участок BC (0 £ х £  )
)
Q z (x)= V B - qx = q ∙ l/2- qx и
My (x)= VB∙x - q∙x∙x /2 = q∙ l/2∙x - q∙x2 /2
5) Определяем ординаты поперечных сил и изгибающих моментов в начале и на конце балки:
Поперечная сила линейно зависит от х и для построения эпюры Qz достаточно определить две ординаты. При х=0, имеем
Qz(0= q l /2, а при x =  Qz(l)= = q∙ l -q l /2 = -q l /2.
Qz(l)= = q∙ l -q l /2 = -q l /2.
Отложим эти значения от нулевой прямой под опорами балки (ординату положительного знака - вверх, а ординату отрицательного знака - вниз) и соединим их вершины прямой линией, которая наклонена к оси балки (рис.11.11,в). Эта прямая пересекает нулевую прямую по середине пролета балки, то есть в этом сечении балки поперечная сила равняется нулю и согласно дифференциальной зависимости изгибающий момент достигает максимального значения.
Изгибающий момент имеет квадратичную зависимость от х, поэтому нужно определить, по меньшей мере, три ординаты этой эпюры (под опорами балки и по середине пролета):
при х=0 имеем My(0) = 0,
при х=  /2 имеем
/2 имеем
My(l /2)=q∙ l / 2 ∙ l/2 - q(l /2)2/2 = q l 2 / 8
при х= l получим My(l) = 0.
Чтобы начертить точнее эпюру изгибающих моментов нужно определить ее ординаты в сечениях, расположенных на расстояниях l/4 от опор балки:
My(l /4) = My(3l/4) = q ∙ l / 2∙l/4- q(l /4)2/2=3/4∙ q l 2 / 8
На рисунке11,11,г построена эпюра изгибающих моментов.
Метод сечений дает возможность построить эпюры поперечных сил и изгибающих моментов, для какой угодно балки или другой стержневой системы, например, рамы или арки. Но следует помнить, что при большом количестве участков уравнения внутренних усилий имеют сложный характер и при определении ординат усилий возможные ошибки в расчетах.
Для упрощения построения эпюр поперечных сил и изгибающих моментов, в какой либо балке, можно использовать практический метод площадей. Рассмотрим основные положения и последовательность использования этого метода.
Метод площадей: Он базируется на использовании дифференциальных зависимостей между внутренними усилиями и интенсивностью внешней нагрузки и заключается в определении этих усилий в сечениях балки, взятых на границах участков (то есть на конце предыдущего и в начале последующего участков). Независимо от количества участков балки усилия всегда определяются суммой двух величин.
Установим связь между поперечными силами  на конце и
на конце и 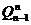 в начале какого-нибудь участка n, который имеет длину a n и загружен равномерно распределенной нагрузкой q, направленной вверх (рис.11.12,а).
в начале какого-нибудь участка n, который имеет длину a n и загружен равномерно распределенной нагрузкой q, направленной вверх (рис.11.12,а).
Составим уравнение равновесия этого участка, используя условие:


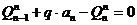 , откуда получим:
, откуда получим:
 (11.6)
(11.6)
Произведение q·a n равняется площади распределенной нагрузки в пределах участка. Это дает возможность сформулировать первое правило метода площадей:
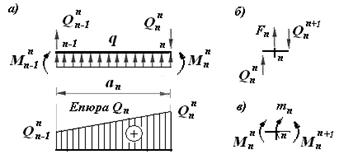
Рис.11.12
Поперечная сила в конечном сечении произвольного участка равняется алгебраической сумме поперечной силы в начальном сечении этого участка и площади распределенной нагрузки в пределах этого участка.
Распределенная нагрузка принимается со знаком плюс (положительной), если действует вверх и со знаком минус (отрицательной), если действует вниз.
Рассмотрим дальше два сечения балки очень близкие к границе n между двумя участками. Левое сечение принадлежит предыдущему участку n, а правое сечение принадлежит последующему участку n+1. На границе этих участков может быть приложена сосредоточенная сила F n (рис.11.12,б). Эта сила также принимается с положительным знаком, если направленная вверх и с отрицательным знаком, если направленная вниз.
Используя условие равновесия  , найдем:
, найдем:
 ,откуда
,откуда  (11.7)
(11.7)
Формула (11.7) дает возможность сформулировать второе правило метода площадей:
Поперечная сила в начальном сечении любого последующего участка равняется алгебраической сумме поперечной силы в конечном сечении предыдущего участка и сосредоточенной силы F n, которая действует на границе этих участков.
Если на границе двух участков отсутствует сосредоточенная сила, то поперечные силы в конечном сечении предыдущего участка и в начальном сечении последующего участка имеет одинаковое значение, то есть  .
.
Установим связь между изгибающим моментами  в конечном сечении участка, изгибающим моментом
в конечном сечении участка, изгибающим моментом  в начальном сечении произвольного участка n, и поперечными силами, которые действуют в тех же сечениях (рис.11.12,а). Составим уравнение равновесия этого участка, используя условие:
в начальном сечении произвольного участка n, и поперечными силами, которые действуют в тех же сечениях (рис.11.12,а). Составим уравнение равновесия этого участка, используя условие: 

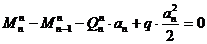 , откуда
, откуда
 , или
, или

окончательно имеем:
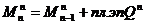 (11.8)
(11.8)
Таким образом, имеем возможность сформулировать третье правило метода площадей:
Изгибающий момент в конечном сечении произвольного участка равняется алгебраической сумме изгибающего момента в начальном сечении этого участка и площади э пюры поперечных сил в пределах этого участка.
Если на границе двух участков действует сосредоточенный момент m n, то связь между ним и изгибающими моментами в двух безгранично близких сечениях балки найдем из условия равновесия:  (рис.11.12,в).
(рис.11.12,в).  , откуда
, откуда
 (11.9)
(11.9)
Формула (11.9) дает возможность сформулировать четвертое правило метода площадей:
Изгибающий момент в начальном сечении любого последующего участка равняется алгебраической сумме изгибающего момента в конечном сечении предыдущего участка, и сосредоточенного момента, который действует на границе этих участков.
Величины и знаки поперечной сила и изгибающего момента в начальном сечении крайнего левого участка балки всегда известны. Они равняются соответственно сосредоточенной силе и сосредоточенному моменту в этом сечении с соответствующими знаками. Рассматриваем это как пятое правило метода площадей.
Пять правил метода площадей, позволяют определить поперечные силы и изгибающие моменты в граничных сечениях участков балки последовательно, начиная от левого края и построить эпюры этих усилий.
Пример 5.6. Последовательность построения эпюр поперечных сил и изгибающих моментов методом площадей проследим на примере балки, размеры и нагрузки которой показаны на рис.11.13,а.
1) Определяем опорные реакции VВ и VС балки, используя рациональные условия равновесия:
 ,
,  , откуда
, откуда

 ,
,  , откуда
, откуда

2) Делим балку на участки так, чтобы в пределах распределенных нагрузок было не меньше двух участков равной длины. Остальные участки балки разграничиваются так же, как и в методе сечений. В данном случае целесообразно разделить балку на 7 участков, как показано на рис.11,13,б. Сечения балки, которые совпадают с границами участков, обозначаем цифрами от 0 до 7 (последняя цифра всегда равняется количеству участков балки).
3) Определяем поперечную силу и изгибающий момент на левом конце балки, то есть в разрезе 0 балки. Из расчетной схемы балки имеем: 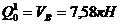 , а
, а  .
.
4) Определяем последовательно поперечные силы в сечениях 1,2,3…, используя правила 1 и 2, или формулы (11.6) и (11.7):
- участок 1(0-1): a1=1м, q=0,  , тогда:
, тогда:
 (по формуле 11.6);
(по формуле 11.6);

Рис.5.13
- участок 2(1-2): a2=1м, q=-4кН/м,  (по формуле 11.7 при F1=0), тогда:
(по формуле 11.7 при F1=0), тогда:  (по формуле 11.6);
(по формуле 11.6);
- участок 3(2-3): a3=1м, q=-4кН/м,  (по формуле 11.7 при F2=0), тогда:
(по формуле 11.7 при F2=0), тогда:  (по формуле 11.6);
(по формуле 11.6);
- участок 4(3-4): a4=1м, q=-4кН/м,  (по формуле 11.7 при F3=0), тогда:
(по формуле 11.7 при F3=0), тогда:  (по формуле 11.6);
(по формуле 11.6);
- участок 5(4-5): a5=1м, q=0,  (по формуле 11.7 при F4=0), тогда:
(по формуле 11.7 при F4=0), тогда:  , (по формуле 11.6);
, (по формуле 11.6);
- участок 6(5-6): a6=0,5м, q=5,  (по формуле 11.7 при F5= -7кН), тогда:
(по формуле 11.7 при F5= -7кН), тогда:
 , (по формуле 11.6);
, (по формуле 11.6);
- участок 7(6-7): a7=0,5м, q=5,  (по формуле 5.7 при F6=0), тогда:
(по формуле 5.7 при F6=0), тогда:
 , (по формуле 11.6).
, (по формуле 11.6).
Используем вычисленные величины для построения эпюры поперечных сил (рис.11.13,в).
5) Определяем последовательно изгибающие моменты в сечениях 1,2,3…, используя правила 3 и 4, или формулы (11.8) и (11.9):
- участок 1(0-1): a1=1м,  ,
,  ,
,  , тогда:
, тогда:  (по формуле 11.8);
(по формуле 11.8);
- участок 2(1-2): a2=1м,  ,
,  ,
, 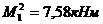 (по формуле 11.9), тогда:
(по формуле 11.9), тогда:
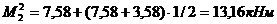 (по формуле 11.8);
(по формуле 11.8);
- участок 3(2-3): a3=1м,  ,
,  ,
, 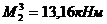 (по формуле 11.9), тогда:
(по формуле 11.9), тогда:
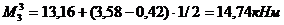 (по формуле 11.8);
(по формуле 11.8);
- участок 4(3-4): a4=1м,  ,
, 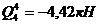 ,
,  (по формуле 11.9), тогда:
(по формуле 11.9), тогда:
 (по формуле 11.8);
(по формуле 11.8);
- участок 5(4-5): a5=1м,  ,
,  ,
,  (по формуле 11.9), тогда
(по формуле 11.9), тогда
 (по формуле 11.8);
(по формуле 11.8);
- участок 6(5-6): a6=0,5м, 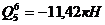 ,
,  ,
,  (по формуле 11.9), тогда:
(по формуле 11.9), тогда:
 (по формуле 11.8);
(по формуле 11.8);
- участок 7(6-7): a7=0,5м,  ,
,  ,
,  (по формуле 11.9),
(по формуле 11.9),
 (по формуле 11.8).
(по формуле 11.8).
Используем вычисленные величины для построения эпюры изгибающих моментов (рис.11.13,г).
При наличии определенного опыта использования приведенных выше правил и формул, можно строить эпюры поперечных сил и изгибающих моментов, выполняя последовательно необходимые подсчеты и записывая величины ординат эпюр в принятых сечениях балки.






