Верещагина
Эпюры изгибающих моментов в действительном состоянии балки, в зависимости от нагрузки, могут быть ограничены кривыми линиями (чаще всего квадратичной параболой, или ее частью), а также прямыми линиями.
Рис.11.27
Поэтому на любом участке балки эпюра изгибающих моментов может состоять из следующих простых фигур: прямоугольника, треугольника, вогнутой квадратичной параболы (или её половины), выгнутой квадратичной параболы (или её половины). На рис.11.27 приведены формулы для определения площадей этих фигур и координаты центров тяжести. Если на каком-то участке эпюра имеет форму трапеции, то ее легко разделить на два треугольника и рассматривать каждый из них отдельно при выполнении процесса перемножения эпюр.
Эпюры изгибающих моментов в единичном (возможном) состоянии балки всегда имеют прямолинейную форму на любом участке балки, то есть форму прямоугольника, треугольника или трапеции. При определении ординат этих фигур под центрами тяжести какой-либо фигуры действительного состояния используем соотношение между координатами центров тяжести и длинами участков.
Рассмотрим общий случай, когда на каком-то участке действительного состояния эпюра изгибающих моментов криволинейная и на концах участка имеет ординаты h1 и h2, а эпюра изгибающих моментов единичного состояния на этом участке имеет форму трапеции с ординатами b1 и b2. Обозначим длину участка через а (рис.11.28). Чтобы перемножить эти эпюры по правилу Верещагина, разделим первую епюру (в заданном состоянии) на три фигуры: квадратичную параболу 1 и два треугольника 2 и 3.
Рис.11.28
Как видно из рисунка 11.28 все простые фигуры имеют общее основание, равное а, и разные высоты. Используя известные формулы (рис.11.27), определяем площади трех фигур действительного состояния балки: ω1=2/3a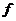 
; ω2=1/2ah1; ω3=1/2ah2.Координаты центров тяжести этих фигур известны, они приведены на рис. 11.28.
Определим ординаты эпюры единичного состояния под центрами тяжести каждой части эпюры действительного состояния, используя соотношение расстояний центров тяжести от начала и конца участка к длине участка. Эти ординаты соответственно равняются:
y1 =1/2(b1+ b2); y2 =2/3b1+1/3b2; y3 =1/3b1+2/3 b2.
Перемножим площади отдельных частей эпюры заданного состояния на соответствующие ординаты эпюры единичного состояния и найдем сумму этих величин. Тогда получим общую формулу умножения этих эпюр по правилу Верещагина:
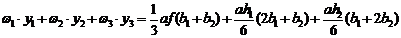, или
(11.65)
Формула (11.65) применяется в любом случае, то есть при любых значениях ординат 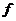, h1, h2, b1, и b2 (положительных, отрицательных, или нулевых).
При перемножении эпюр изгибающих моментов с использованием формулы (11.65) нужно разделить эпюры изгибающих моментов на простые фигуры в пределах каждого участка, определить в действительном состоянии площади этих фигур и положения их центров тяжести, а также найти ординаты эпюры в единичном состоянии под центрами тяжести эпюры действительного состояния.
Для определения перемещения необходимо разделить величину, найденную по формуле (11.65) на жесткость соответствующего участка балки.
Задание 11.1 для самостоятельной работы: Для заданных расчетных схем балок построить эпюры поперечных сил и изгибающих моментов и определить размеры поперечных сечений двутавровой формы из условия прочности, если расчетное сопротивление равняется 210 МПа.
Балка 1.
Балка 2.
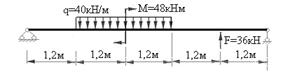
Балка 3.
Балка 4.
Балка 5.
Задание 11.2 для самостоятельной работы: Построить эпюры прогибов и углов поворота для балок 1 и 5.
Задание 11.3 для самостоятельной работы: Определить прогиб и угол поворота правого торца балки 3 и левого торца балки 4, пользуясь правилом Верещагина.
5.16 Вопрос для проверки знаний
1. Что такое балка? Какие разновидности балки Вы знаете?
2. Какие типы опор принимаются для закрепления балки?
3. В каком случае балка является статически определимой?
4. Как определяются опорные реакции балки?
5. Чему равняется горизонтальная реакция неподвижной опоры при вертикальной нагрузке балки?
6. Как проверить найденные реакции?
7. Чем отличается прямой изгиб балки от косого?
8. Что зовется чистым изгибом балки?
9. Какие внутренние усилия возникают в поперечных сечениях балки при чистом и при поперечном изгибе?
10. Что такое поперечная сила? Какое правило знаков принимается для нее?
11. Что такое изгибающий момент? Какое правило знаков принимается для него?
12. Как определяется поперечная сила в произвольном сечении балки?
13. Как определяется изгибающий момент в каком-нибудь сечении балки?
14. Что называется эпюрой поперечных сил и эпюрой изгибающий моментов?
15. Что выражают ординаты эпюр поперечных сил и изгибающий моментов?
16. Какие методы построения эпюр внутренних усилий существуют?
17. В чем заключается метод сечений? В какой последовательности реализуется этот метод?
18. В чем заключается метод площадей? В какой последовательности реализуется этот метод?
19. В чем заключается проверка построенных эпюр поперечных сил и изгибающий моментов?
20. Какие дифференциальные зависимости существуют между внутренними усилиями и внешней нагрузкой?
21. Докажите дифференциальные зависимости между внутренними усилиями и внешней нагрузкой.
22. Чему равняется поперечная сила в сечениях балки, в которых изгибающий момент достигает экстремальных значений?
23. Как изменяется изгибающий момент на участках балки, где поперечная сила равняется нулю?
24. Как изменяется изгибающий момент на участках балки, где поперечная сила линейно зависит от абсциссы сечения?
25. Как изменяется поперечная сила на участках, свободных от распределенной нагрузки?
26. Как изменяется эпюра поперечных сил в сечении балки, в котором приложена внешняя сосредоточенная сила?
27. Как изменяется эпюра изгибающий моментов в сечении балки, где действует внешний сосредоточенный момент?
28. Как определяется максимальное значение изгибающего момента?
29. Какие напряжения возникают в поперечном сечении балки при чистом изгибе? Как они определяются и как изменяются по высоте сечения?
30. Что такое нейтральный слой и нейтральная ось?
31. Что такое жесткость балки при изгибе? Какие единицы измерения она имеет?
32. Что такое момент сопротивления поперечного сечения при изгибе? Как он определяется и в каких единицах измеряется?
33. Как определяются нормальные напряжения в поперечном сечении балки при поперечном изгибе?
34. Как определяются касательные напряжения в поперечном сечении балки при поперечном изгибе?
35. Какой вид имеет эпюра касательных напряжений в сечении прямоугольной и двутавровой формы?
36. Что такое главные напряжения при поперечном изгибе? Как они определяются?
37. Запишите условие прочности при изгибе? Какие задачи решают с использованием этого условия?
38. Какие формы поперечного сечения являются рациональными для балки из пластичного материала?
39. Какие формы поперечного сечения являются рациональными для балки из хрупкого материала?
40. Как вывести дифференциальное уравнение изогнутой оси балки?
41. Как определяют углы поворота и прогибы сечений балки методом непосредственного интегрирования дифференциального уравнения?
42. Как определяются неизвестные постоянные интегрирования при использовании метода непосредственного интегрирования дифференциального уравнения?
43. Как определяют углы поворота и прогибы сечений балки методом начальных параметров?
44. Как определяются неизвестные начальные параметры при изгибе?
45. Какие дифференциальные зависимости существуют между углами поворота и прогибами балки?
46. Как определяются прогибы и углы поворота методом Мора-Максвелла?
47. Что такое правило Верещагина? Как оно применяется для определения угловых и линейных перемещений?
ГЛАВА XII. КРУЧЕНИЕ ПРЯМОГО БРУСА
