Рассмотрим некоторую балку, загруженную распределенной нагрузкой переменной интенсивности q(x) и произвольными сосредоточенными силами и моментами (рис.11.6).
Проведем два поперечных сечения балки, взятые соответственно на расстояниях x и x+dx от начала координат, на участке, где действует распределенная нагрузка q(x).
Рис.11.6
Выделим и начертим отдельно бесконечно малый элемент балки длиной dx (рис.11.7). Покажем все нагрузки, действующие на этот элемент балки. В левом сечении этого элемента действуют усилия Qz(x) и My(x), а в правом сечении будут действовать усилия Qz(x) + d Qz (x) и My(x) + d My (x) соответственно, то есть при переходе от одного сечения к другому, усилию получают некоторые бесконечно малые приращения. Ввиду малой длины элемента dx, можно считать, что внешняя нагрузка q(x) в пределах этого элемента изменяется прямолинейно или имеет даже постоянную интенсивность q.
Рис. 11.7
Заметим, что направления внутренних усилий и внешней нагрузки q(x), которые показаны на рис.11.7 соответствуют положительным знакам этих усилий.
Составим два уравнения равновесия с использованием следующих условий:
и 
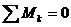, где К является центром правого сечения балки, а ось z направлена вверх.
, откуда находим:
(11.3)
, откуда:
(11.4)
или
(11.5)
Полученные зависимости (11.4) и (11.5) являются дифференциальными зависимостями между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки. На их основе можно сформулировать следующие выводы:
1) Первая производная от изгибающего момента по абсциссе x равняется поперечной силе. Эта зависимость является справедливой для произвольного поперечного сечения балки и позволяет выявить некоторые свойства эпюр поперечных сил и изгибающих моментов:
Если поперечная сила на некотором участке балки равна нулю, то изгибающий момент на этом участке имеет постоянную величину, то есть эпюра изгибающих моментов ограничена прямой, параллельной оси балки.
Если поперечная сила на некотором участке балки имеет постоянную величину, то изгибающий момент на этом участке находится в линейной зависимости от положения сечения, то есть эпюра изгибающих моментов ограничена прямой, наклоненной к оси балки под углом, тангенс которого равняется поперечной силе.
Если поперечная сила на некотором участке изменяется по линейному закону, то изгибистый момент на этом участке изменяется по закону квадратичной параболы, то есть эпюра M y(x) ограничена квадратичной параболой, вершина которой расположена под сечением балки, в котором поперечная сила равняется нулю. При этом, на участках балки, где поперечная сила имеет положительный знак, изгибающий момент увеличивается (возрастает), а на участках балки, где поперечная сила имеет отрицательный знак, изгибающий момент убывает.
Таким образом, изгибающий момент достигает максимального значения в сечении балки, где поперечная сила равняется нулю или меняет свой знак с положительного на отрицательный. Если поперечная сила при переходе через нулевое значение изменяет свой знак из отрицательного на положительный, то изгибающий момент достигает минимального значения в сечении балки, где поперечная сила равняется нулю.
2) Первая производная от поперечной силы по абсциссе x или вторая производная от изгибающего момента по той же абсциссе равняется интенсивности распределенной нагрузки. Эта зависимость позволяет выявить некоторые дополнительные свойства эпюр поперечных сил и изгибающих моментов:
Если интенсивность распределенной нагрузки на некотором участке балки равняется нулю q(x)=0, то поперечная сила на этом участке имеет постоянную величину, а изгибающий момент изменяется по линейному закону.
Если интенсивность распределенной нагрузки на некотором участке балки имеет постоянную величину q, то поперечная сила линейно зависит от абсциссы x, а изгибающий момент изменяется по уравнении квадратной параболы.
Дифференциальные зависимости (11.4) и (11.5) используют при построении эпюр внутренних усилий при изгибе, а также при осуществлении проверки построенных епюр.
