Рассмотрим плоское сечение бруса произвольной формы относительно произвольной системы координат y0z. Момент инерции этого сечения относительно оси y будет определяться интегралом:
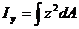
Обозначим среднее значение интеграла через  и используем теорему о среднем значении интеграла. В результате получим:
и используем теорему о среднем значении интеграла. В результате получим:
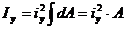 , откуда
, откуда  , или
, или
 (8.31)
(8.31)
аналогично  (8.32)
(8.32)
Величины i y и i z являются радиусами инерции сечения относительно соответствующих осей координат. Радиусы инерции сечения относительно главных центральных осей являются главными радиусами инерции. Они имеют экстремальные значения  и
и  .
.
 и
и  (8.33)
(8.33)
Радиус инерции является удобной геометрической характеристикой плоского сечения. С его помощью можно геометрически исследовать изменение моментов инерции в зависимости от положения осей, то есть от их поворота. Для этого нужно определить  и
и  и построить эллипс инерции на главных осях. Положим, что ось максимальной инерции u расположена горизонтально, а ось минимальной инерции сечения – вертикально.
и построить эллипс инерции на главных осях. Положим, что ось максимальной инерции u расположена горизонтально, а ось минимальной инерции сечения – вертикально.
Отложим от центра сечения в двух направлениях отрезок  перпендикулярно оси максимальной инерции u. Получим большую ось эллипса. Потом отложим отрезок
перпендикулярно оси максимальной инерции u. Получим большую ось эллипса. Потом отложим отрезок  перпендикулярно оси минимальной инерции v в двух направлениях и получим малую ось эллипса.
перпендикулярно оси минимальной инерции v в двух направлениях и получим малую ось эллипса.
Построим эллипс, пользуясь правилами начертательной геометрии (рис. 8.10) и покажем, как при его использовании определяется момент инерции относительно произвольной оси y, проведенной под углом α оси u. Проведем касательную к эллипсу параллельно осе y. Она пройдет через точку Д эллипса. Опустим из центра О перпендикуляр ОС к этой касательной. Отрезок ОС есть радиус инерции  в масштабе чертежа, тогда
в масштабе чертежа, тогда  . Аналогично определяются моменты инерции сечения относительно произвольной оси.
. Аналогично определяются моменты инерции сечения относительно произвольной оси.
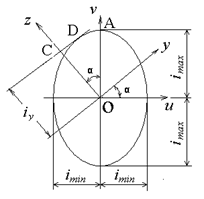
Рис. 8.10
Моменты сопротивления.
Моментом сопротивления поперечного сечения относительно какой-нибудь оси зовется отношение момента инерции относительно данной оси к расстоянию наиболее отдаленной точки сечения от этой оси. Обозначим момент сопротивления относительно оси y через W y, а расстояние наиболее отдаленной точки сечения от этой оси через z max, тогда будем иметь:
 (8.34)
(8.34)
Пользуясь этим правилом, определим моменты сопротивления прямоугольного (рис.8.5), треугольного (рис.8.6), и круглого (рис.8.7) поперечных сечений относительно главных центральных осей y и z.
Для прямоугольного сечения имеем:
 ,
, 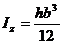 ,
, 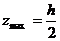 ,
,  , тогда:
, тогда:
 ,
,  (8.35)
(8.35)
Для треугольного сечения:
 ,
, 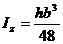 ,
, 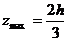 ,
,  , тогда:
, тогда:
 ,
,  (8.36)
(8.36)
Для круглого сечения:
 ,
,  , тогда:
, тогда:
 (8.37)
(8.37)
Момент сопротивления является важной геометрической характеристикой плоских сечений и используется при расчетах на прочность элементов инженерных сооружений и машин, которые подвержены изгибу. Единицами измерения момента сопротивления являются см3 или м3.
Для поперечного сечения круглой формы определяется полярный момент сопротивления, который равняется отношению полярного момента инерции к радиусу сечения. Учитывая, что
 , а
, а  , получим:
, получим:
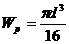 (8.38)
(8.38)
Пример 8.2: Для поперечного сечения, состоящего из двутавра №16 и прямоугольника со сторонами 1 см и 24 см (рис.8.11), требуется:
1) определить осевые моменты и центробежный момент инерции относительно центральных осей  и
и  ;
;
2) определить положение главных осей инерции и величины главных осевых моментов инерции;
3) определить главные радиусы инерции и главные моменты сопротивления
Последовательность решения задачи: Учитывая, что положение центра тяжести заданного сечения было уже найдено (смотри пример 8.1), решение задачи осуществляем в такой последовательности:
1) Выписываем геометрические характеристики двутавра №16 (из таблицы ГОСТ 8240-89) и определяем геометрические характеристики прямоугольника с размерами сторон 1х24:
А1= 20,2 см2;  см4;
см4;  см4;
см4; 

Рис.8.11
А2=1·24=24см2; 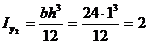 см4;
см4;
 см4;
см4; 
2) Определяем расстояния между центральными осями всего сечения и параллельными к ним собственными осями каждой части этого сечения:
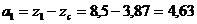 см;
см;
 см;
см;
 см;
см;
 см.
см.
3) Определяем осевые и центробежный моменты инерции сечения относительно центральных осей  и
и  :
:
 см4;
см4;
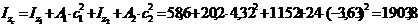 см4;
см4;
 см4.
см4.
4) Определяем положение главных центральных осей инерции сечения:
 ;
;
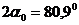 ;
; 
Таким образом, чтобы получить положение главных осей инерции сечения нужно центральные оси повернуть на угол 40,450 против часовой стрелки.
Ось максимальной инерции получаем при повороте центральной оси, относительно которой момент инерции имеет больше значения. В данном случае  , поэтому ось u будет осью максимальной инерции, а перпендикулярная к ней ось v будет осью минимальной инерции.
, поэтому ось u будет осью максимальной инерции, а перпендикулярная к ней ось v будет осью минимальной инерции.
5) Определяем главные моменты инерции заданного сечения по формулам (8.30):
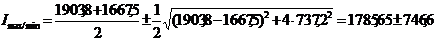 ;
;
Откуда:
 см4;
см4;
 см4
см4
Проверим эти величины. Существует две проверки:
1. сумма моментов инерции относительно двух взаимно перпендикулярных центральных осей остается постоянной величиной при повороте осей, т.е.
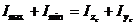 ;
;
 , это равенство выполняется.
, это равенство выполняется.
2.Максимальный и минимальный моменты инерции определяем соответственно по формулам (8.26) и (8.25):
 ,
,
 , где
, где
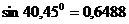 ,
,  ,
, 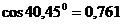 ,
,  и
и
 ,тогда:
,тогда:
 см4
см4
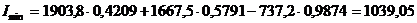 см4
см4
Эти величины полностью совпадают с величинами, определенными по формуле (8.30).
6) Определяем главные радиусы инерции, используя формулы (8.33):
 см;
см;
 см.
см.
7) Определяем главные моменты сопротивления. Для этого необходимо определить расстояния от главных осей инерции до наиболее отдаленных точек сечения. Рассматривая чертеж сечения, легко заметить, что его точка С больше всего удалена от оси u, а точка D больше всего удалена от оси v. Найдем эти расстояния по формулам (8.24)
 ,
, 
 см,
см,  см,
см,
 см,
см,  см,
см,
тогда: 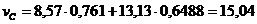 см,
см,
 см
см
Определяем моменты сопротивления относительно главных центральных осей u и v:
 см3;
см3;
 см3
см3

Рис.8.12 Рис.8.13
2.8 Задание для самостоятельной работы: 1) Для поперечного сечения балки, составленного из двух прокатных швеллеров № 24, соединенных полками согласно рисунку 8.12, нужно определить геометрические характеристики. 2) Определить геометрические характеристики поперечного сечения, форма и размеры которого (в сантиметрах) показаны на рис.8.13.




