Моменты инерции равнобедренного треугольника относительно центральных осей, одна из которых параллельная основанию b треугольника.

                     

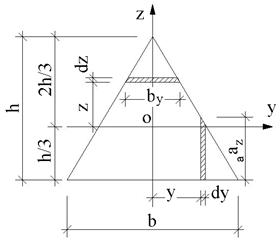
                                                          Рис. 8.6

На рис.8.6 начерчен равнобедренный треугольник, центр тяжести которого находится в точке О на расстоянии 2/3h от вершины. Для определения момента инерции этого треугольника относительно горизонтальной оси y, проведенной через его центр тяжести, выделим на расстоянии z от оси y элементарную часть площади шириной b _y и высотой dz. Из соотношения сторон подобных треугольников находим: 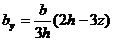  , тогда

                            

Окончательно имеем: 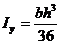                                                                                   (8.16)                           

       Для определения момента инерции относительно вертикальной оси z выделим на расстоянии y от нее элементарную часть площади высотой a _z и шириной dy. Из соотношения сторон подобных треугольников находим: 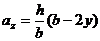, тогда

                                 

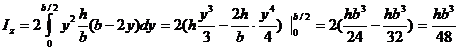
Окончательно 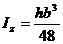                                                                                         (8.17) 

 

Моменты инерции круга относительно центральных осей и центра (полюса).

 

Определим сначала полярный момент инерции круга, радиус которого равняется r, а диаметр d(рис. 8.7). Для этого выделим из круга элементарное кольцо толщиной dρи радиусом ρ. Элементарная площадь этого кольца равняется dA =2 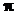ρdρ. Подставим это значение в формулу (8.11) и найдем интеграл полученного произведения в пределах изменения ρот нуля до r:

                                        

                                              

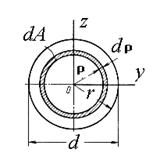
                                                           Рис. 8.7

 

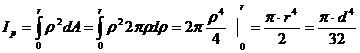                                                   (8.18)

       Ввиду симметрии круга относительно центральных осей y и z, имеем 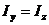, или 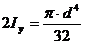      , откуда:

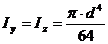                                                                                                         (8.19)

                                                           

 

Зависимость между моментами инерции

Относительно параллельных осей.

 

Определим моменты инерции сечения произвольных размеров и формы (рис.8.8) относительно произвольных осей y и  z, если известные осевые и центробежный моменты инерции этого сечении относительно собственных центральных осей y_с и  z_{с ,} то есть если известные следующие моменты инерции:

                    ; ;

                                     

 

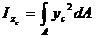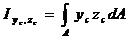
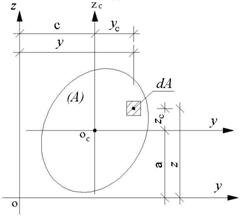
                                                      Рис. 8.8

 

Выделим элементарную часть dA площади сечения и найдем зависимость между ее координатами в двух системах (yОz) и (y_сО_сz_с).

Из рис.8.8 следует, что 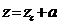; 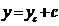. Используем формулы (2.9), (2.10) и (2.13):

 

            

                                               +

 

            

                                   + =    

                                               

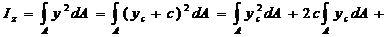
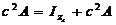
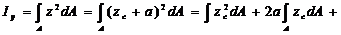
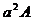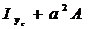
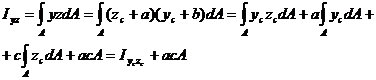
В результате получаем формулы взаимной связи между моментами инерции относительно параллельных осей, одна из которых центральная, т.е. проходит через центр тяжести сечения:

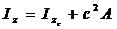                                                                                                            (2.20)

                                                                                                            (2.21)

                                                                                                         2.22)                                         

Таким образом, можем сформулировать следующие правила, по которым определяются осевые моменты и центробежный момент инерции относительно параллельных осей, одна из которых проходит через центр тяжести сечения:

Момент инерции сечения относительно произвольной оси равняется сумме момента инерции относительно параллельной к ней центральной оси и произведения площади сечения на квадрат расстояния между этими осями.

Центробежный момент инерции относительно произвольной пары осей равняется сумме центробежного момента инерции относительно параллельных к ним центральных осей и произведения площади сечения на расстояния между двумя парами параллельных осей.