Методы расчета бруса на прочность, жесткость и устойчивость создаются с использованием следующих гипотез, т.е. утверждений, которые не нуждаются в доказательстве. Существуют 7 основных гипотез сопротивления материалов:
- Гипотеза сплошности и однородности. Она предусматривает, что материал бруса является однородным, полностью заполняет весь объем бруса и имеет одинаковые свойства во всех точках. Эта гипотеза позволяет рассматривать свойства безгранично малого элемента материального тела (конструкции) эквивалентными свойствам всего объема тела реальных размеров.
- Гипотеза изотропности. Материал бруса является изотропным, если он имеет одинаковые физические и механические свойства во всех направлениях. Эта гипотеза может быть использована при решении большинства задач сопротивления материалов. Но следует помнить, что существуют в природе анизотропные материалы, свойства которых в разных направлениях разные. В некоторых случаях нужно учитывать эти свойства анизотропных материалов.
- Гипотеза идеальной упругости материалов. Согласно этой гипотезе брус (элемент какой-нибудь конструкции) полностью возобновляет начальную форму и размеры после того, как исчезнут причины, которые вызвали деформации бруса. Деформации бруса, изготовленного из идеально упругого материала, зависят от нагрузок, которые действуют на него в любое время и не зависят от последовательности приложения нагрузки к брусу.
- Гипотеза малости деформаций. Опыт подтверждает, что деформации бруса являются очень малыми по сравнению с его первоначальными размерами. Это обстоятельство позволяет не учитывать возможные изменения расположения нагрузок бруса при его деформации. То есть, расстояния между нагрузкой бруса и какими-либо его точками остаются неизменными.
- Гипотеза линейности деформаций и напряжений. При деформации бруса имеет место и всегда сохраняется линейная (прямо пропорциональная) зависимость между напряжениями и деформациями. Эта гипотеза впервые сформулирована Р. Гуком и имеет название закона Гука. Для большинства материалов этот закон выполняется, но при напряжениях, которые не превышают границы пропорциональности.
- Гипотеза независимости действия нагрузок (принцип суперпозиции). Согласно этому принципу, перемещения точек бруса, возникающие от действия нескольких сил равняется сумме перемещений, возникающих от действия каждой силы сечения отдельно.
Рассмотрим три случая нагружения балки (рис.7.8):
а) балка нагружена двумя силами F1 и F2 одновременно;
б) балка нагружена силой F1 ;
в ) балка нагружена силой F2.
Допустим, что при одновременном действии сил F1 и F2 некоторая точка С балки переместится в положение С1, то есть получит перемещение СС1 =Δ.При нагрузке балки силой F1 точка С переместится в положение С2, то есть получит перемещение СС2 = Δ 1, а при нагрузке балки силой F2 точка С переместится в положение С3, то есть получит перемещение СС3 = Δ 2. При этом сумма перемещений Δ 1 и Δ 2 будет равняться перемещению Δ.
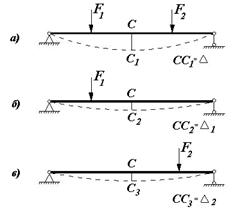
Рис. 7.8
- Гипотеза плоских сечений. Если взять плоское сечение бруса до его нагружения, то это сечение останется плоским и после нагружения, вследствие которого наступает деформация бруса. Эта гипотеза называется гипотезой Бернулли и имеет широкое использование в сопротивлении материалов. Доказательство большинства формул сопротивления материалов выполняется на основе этой гипотезы.
Виды деформации бруса.
В зависимости от нагрузок, действующих на брус, в любом его поперечном сечении могут возникать от одной до шести составляющих внутренних усилий. В большинстве задач сопротивления материалов нагрузки действуют в одной из плоскостей бруса и вызывают простые или сложные виды его деформации.
К простым видам деформации относят:
1. Растяжение или сжатие прямого бруса;
2. Чистый сдвиг;
3. Чистый и поперечный изгиб;
4. Кручение.
К сложным видам деформации бруса относят:
1. Косой изгиб бруса;
2. Внецентренное растяжение или сжатие;
3. Изгиб с кручением;
4. Изгиб с растяжением или сжатием.
В следующих главах будут рассмотрены простые и сложные виды деформации. Для каждого вида деформации бруса, будут приведены:
- методы определения внутренних усилий, которые возникают в его поперечных или наклоненных сечениях от действия внешних нагрузок;
- методы определения нормальных, касательных и главных напряжений, которые возникают в отдельных точках сечения;
- методы определения перемещений и деформаций и методы расчета бруса на прочность, жесткость и устойчивость с использованием соответствующих условий.
Вопросы для проверки полученных знаний.
1. Что называется брусом? Какие разновидности бруса встречаются в сопротивлении материалов?
2. Что такое расчетная схема бруса, и с какой целью она образуется?
3. Что такое нагрузка, действующая на брус? Какие виды нагрузок бывают?
4. В каких единицах измеряется сосредоточенная сила, сосредоточенный момент, распределенные нагрузки?
5. Что такое внутренние усилия? Как выявить внутренние усилия?
6. Какие составляющие внутренних усилий возникают в поперечном сечении бруса? Какое название они имеют?
7. Из каких условий определяются внутренние усилия?
8. Что такое напряжение в точке бруса? Какое название имеют напряжения, которые действуют в плоскости сечения и перпендикулярно этой плоскости?
9. Какая зависимость существует между полным, нормальным и касательным напряжениями, а также между полным касательным напряжением и его составляющими?
10. Что такое линейные и угловые деформации бруса?
11. Что такое абсолютная и относительная деформации? Как они определяются?
12. Какое различие между деформацией и перемещением?
13. Какие основные гипотезы приняты в сопротивлении материалов?
14. Разъясните сущность гипотезы сплошности и однородности тела.
15. Разъясните сущность гипотезы идеальной упругости тела.
16. Разъясните сущность гипотезы плоских сечений.
17. Что такое принцип независимости действия сил?






