Веса стержня
Рассмотрим вертикально расположенный стержень с жестким закреплением внизу и определим продольные силы в его поперечных сечениях от действия собственного веса. Такой стержень называется колонной и очень часто используется в инженерных сооружениях разного назначения. Обозначим площадь поперечного сечения стержня буквой А, длину стержня буквой l, а удельный вес материала стержня буквой γ (рис.9.2,а).
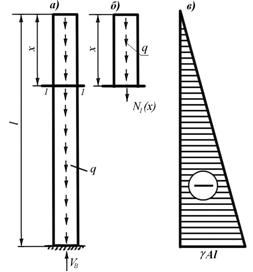
Рис. 9.2
Собственный вес стержня можно считать равномерно распределенной нагрузкой по его длине. Интенсивность этой нагрузки равняется произведению удельного веса γ на площадь поперечного сечения А, то есть q = γA.
Проведем поперечное сечение 1-1 стержня на расстоянии x от начала координат и рассмотрим равновесие верхней части стержня длиной x (рис.9.2,б).
ΣXi =0, N (x) + q x = 0, откуда N (x)= - q x = -γA x.
Таким образом, продольная сила в произвольном сечении с абсциссой x линейно зависит от этой абсциссы, то есть от положения сечения относительно начала координат.
Определим два значения продольной силы при x =0 и x = l. При x =0 имеем N(0) = 0 и при x = l имеем N(l) = - γAl. Полученная продольная сила имеет отрицательный знак, то есть стержень сжат. На рис.9.2,в построена эпюра продольных сил от действия собственного веса стержня. Эта эпюра ограничена прямой линией, которая наклонена к оси стержня. Тангенс угла ее наклона равняется интенсивности распределенной нагрузки, то есть tgα = q = γA. По эпюре продольных сил находят величину и знак этой силы в произвольном сечении стержня. Достаточно для этого определить величину ординаты эпюры в направлении заданного сечения и принять ее со знаком эпюры.
Заметим, что ордината эпюры N(x) в опорном разрезе стержня равняется реакции опоры. Учитывая, что N(l) = - γAl, имеем
VВ = γAl. Эта реакция направлена вверх, в связи с тем, что продольная сила в опорном разрезе стержня отрицательна и вызывает сжатие стержня (рис. 9.2,а).
Замечания:
1) Если стержень нагружен одновременно собственным весом и осевыми сосредоточенными силами, то нужно определить продольные силы на каждом участке в соответствии с требованиями п. 9.1 и 9.2. В этом случае эпюра будет иметь ступенчатую форму с наклоненными сторонами относительно оси стержня.
2) Если стержень на разных участках имеет разные размеры поперечных сечений, то углы наклона эпюры продольных сил будут разными для каждого участка при учете собственного веса.
Пример 9.1. Определить продольные силы и построить эпюру этих сил для стержня ступенчатой формы, если F = 100 кН, q1 = 20 кН/м, q2 = 50 кН/м. Размеры стержня приведены на рис.9.3,а.
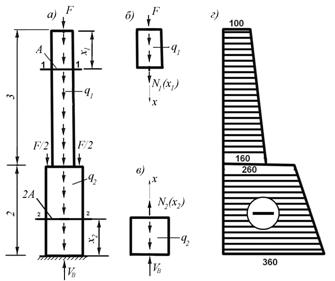
Рис. 9.3
Последовательность решения задачи:
1) Определяем реакцию опоры стержня. Очевидно, что эта реакция направлена вверх и находится из условия равновесия стержня Σ Xi =0. Обозначим реакцию опоры буквой VВ и составим уравнение равновесия:
VВ - 2 F – q1∙ 3 - q2∙ 2 = 0, откуда
VВ = 2 F + q1∙ 3 + q2∙ 2 = 2·100 +20∙3 + 50∙2 = 360 кН.
2) Делим стержень на два участка длиной 3 и 2 м.
3) В пределах каждого участка проводим поперечные сечения 1-1 и 2-2 на расстояниях x1 от верхнего конца стержня и x2 от нижнего конца стержня соответственно.
4) Рассматриваем равновесие верхней части стержня относительно сечения 1-1. Эта часть нагружена силой F, распределенной нагрузкой q1 и неизвестной продольной силой N1(x1), направленной от сечения 1-1, как показано на верхнем рисунке 9.3,б. Определяем продольную силу N1(x1) из условия равновесия:
Σ X i =0, N 1 (x 1)+ F + q 1 x 1 = 0, откуда N 1 (x 1)= - F – q 1 x 1.
При x1=0 находим N1(0) = - F = - 100 кН., а при x1=3 м,находим:
N1(3) = - F - q1∙ 3 = -100-20∙3 = - 160 кН.
5) Рассматриваем равновесие нижней части стержня относительно сечения 2-2. Эта часть нагружена реакцией опоры VВ=360 кН и направленной вверх, распределенной нагрузкой q2 = 50 кН/м и направленной вниз, и неизвестной продольной силой N2(x2), направленной от сечения 2-2, как показано на нижнем рисунке 9.3,в. Определяем продольную силу N2(x2) из условия равновесия:
Σ X i =0, N 2 (x 2)+ VВ - q 2 x 2 = 0, откуда находим:
N 2 (x 2) =\- VВ + q 2 x 2 = -360 + 50∙x2. При x2 =0 имеем N 2 (0) = -360 кН а при x2 =2 м. находим N 2 (2) = -360 + 50∙2 = -260 кН.
6) Используя полученные значения, строим эпюру продольных сил N (рис. 9.3,в).






