Рассмотрим плоское сечения бруса произвольных размеров и формы, площадь которого равняется А (рис.8.4). Проведем через произвольную точку плоскости О горизонтальную y и вертикальную z оси координат и приведем определение и формулы осевых и полярного моментов инерции, а также центробежного момента инерции.
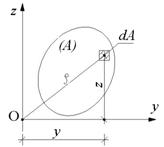
Рис. 8.4
Моментом инерции площади сечения относительно произвольной оси называется интеграл, взятый по всей площади, произведения элементарной части dA этой площади на квадрат ее расстояния от оси.
Выделим элементарную часть dA площади сечения, взятую на расстоянии y от вертикальной оси и на расстоянии z от горизонтальной оси. Тогда, согласно приведенному определению, получим формулы осевых моментов инерции:
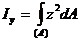(8.9)
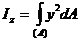(8.10)
Полярным моментом инерции площади сечения бруса относительно произвольной точки (полюса) называется интеграл, взятый по всей площади, произведения элементарной части dA этой площади на квадрат ее расстояния от полюса.
Обозначим через 
расстояние от элементарной части dA площади до полюса О, тогда, согласно приведенному определению, получим формулу:
(8.11)
Легко доказать, что полярный момент инерции относительно начала координат равняется сумме осевых моментов инерции относительно координатных осей y и z. Согласно рис.8.4 имеем: ρ2= y2+ z2. Подставим вместо ρ2 его значение в формулу (8.11), получим:
(8.12)
Таким образом, полярный момент инерции сечения относительно произвольного центра равен сумме осевых моментов инерции относительно координатных осей, проведенных из этого центра.
Центробежным моментом инерции площади сечения относительно двух взаимно перпендикулярных осей называется интеграл, взятый по всей площади сечения, произведения элементарной части dA этого сечения на ее расстояния от координатных осей. То есть:
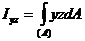(8.13)
Если оси y и z системы координат проведены через центр тяжести сечения и, по крайней мере, одна из этих осей является осью симметрии, то центробежный момент инерции будет равняться нулю.
Осевые, полярный и центробежный моменты инерции измеряются в единицах длины, возведенных в четвертую степени (см4, м4).
Для сечений бруса, которые имеют простую форму, целесообразно использовать известные формулы, выводы которых приводим ниже.
Моменты инерции прямоугольника относительно его центральных осей.
Рассмотрим прямоугольник шириной b и высотой h (рис.8.5). Центр тяжести прямоугольника находится на пересечении диагоналей. Проведем через центр тяжести горизонтальную ось y и вертикальную ось z. Выделим элементарную часть площади шириной b и высотой dz, взятуюна расстоянии z от оси y. Эта элементарная часть площади сечения заштрихована на рисунке и равняется произведению b∙dz, то есть
dA = b∙dz.
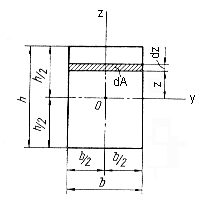
Рис. 8.5
Используем формулу (8.9) и выполним интегрирование в пределах изменения z от нуля до h/2 (в пределах верхней части прямоугольника). Полученный результат удвоим, поскольку ось y является осью симметрии сечения.
I y = 2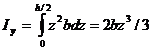 
= 2bz3/3 
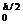
= bh3/12, то есть
(8.14)
Аналогично находим: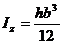 
(8.15)
