Рассмотрим прямой стержень постоянного поперечного сечения, жестко закрепленный сверху. Пусть стержень имеет длину 
и нагружен растягивающей силой F. От действия этой силы длина стержня увеличивается на некоторую величину Δ (рис.9.7,а).
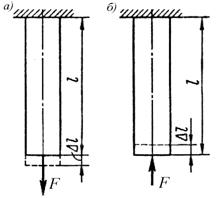
Рис.9.7
При сжатии стержня такой же силой F длина стержня сократится на такую же величину Δ (рис.9.7,б).
Величина Δ , равная разности между длинами стержня после деформации и до деформации, называется абсолютной линейной деформацией (удлинением или укорочением) стержня при его растяжении или сжатии.
Отношение абсолютной линейной деформации Δ к первоначальной длине стержня называется относительной линейной деформацией и обозначается буквой ε или ε x ( где индекс x указывает направление деформации). При растяжении или сжатии стержня величину ε просто называют относительной продольной деформацией стержня. Она определяется по формуле:
(9.8)
Многократные исследования процесса деформирования растянутого или сжатого стержня в упругой стадии, подтвердили существование прямой пропорциональной зависимости между нормальным напряжением и относительной продольной деформацией. Эта зависимость называется законом Гука и имеет вид:
(9.9)
Величина E называется модулем продольной упругости или модулем первого рода. Она является физической постоянной (константой) для каждого вида материала стержня и характеризует его жесткость. Чем больше величина E, тем меньше будет продольная деформация стержня. Величина E измеряется в тех же единицах, что и напряжение, то есть в Па, МПа, и тому подобное. Величины модуля упругости содержатся в таблицах справочной и учебной литературы. Например, величина модуля продольной упругости стали принимается равной E = 2∙105 МПа, а древесины
E = 0,8∙105 МПа.
При расчете стержней на растяжение или сжатие, часто возникает необходимость определения величины абсолютной продольной деформации 
, если известна величина продольной силы, площадь поперечного сечения и материал стержня. Из формулы (9.8) найдем: 
. Заменим в этом выражении ε его значением из формулы (9.9). В результате получим = 
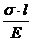. Если использовать формулу нормального напряжения 
, тополучим окончательную формулу для определения абсолютной продольной деформации:
(9.10)
Произведение модуля продольной упругости на площадь поперечного сечения стержня называется его жесткостью при растяжении или сжатии.
Анализируя формулу (9.10) сделаем существенный вывод: абсолютная продольная деформация стержня при растяжении (сжатия) прямо пропорциональная произведению продольной силы на длину стержня и обратно пропорциональная его жесткости.
Заметим, что формула (9.10) может быть использована в том случае, когда поперечное сечение стержня и продольная сила имеют постоянные значения по всей его длине. В общем случае, когда стержень имеет ступенчато переменную жесткость и загружен по длине несколькими силами, нужно разделить его на участки и определить абсолютные деформации каждого из них по формуле (9.10).
Алгебраическая сумма абсолютных деформаций каждого участка будет равняться абсолютной деформации всего стержня, то есть:
(9.11)
Продольные деформации стержня от действия равномерно распределенной нагрузки вдоль его оси (например, от действия собственного веса), определяется следующей формулой, которую приводим без доказательства:
(9.12)
В случае растяжения или сжатия стержня, кроме продольных деформаций возникают также поперечные деформации, как абсолютные, так и относительные. Обозначим через b размер поперечного сечения стержня до деформации. При растяжении стержня силой F этот размер уменьшится на величину Δb, которая является абсолютной поперечной деформацией стержня. Эта величина имеет отрицательный знак.При сжатии, напротив, абсолютная поперечная деформация будет иметь положительный знак (рис. 9.8).
Рис.9.8
Отношение абсолютной поперечной деформации Δb к начальному размеру b называется относительной поперечной деформацией 
.
(9.13)
Опыт показывает, что при напряжениях, которые не превышают предела упругости, относительная поперечная деформация прямо пропорциональна относительной продольной деформации 
и имеет противоположный знак, то есть:
(9.14)
Коэффициент пропорциональности называется коэффициентом поперечной деформации или коэффициентом Пуассона. Его величина характеризует упругие свойства материала и в зависимости от вида материала может изменяться от нуля (для пробки) до 0,5 (для резины). Для различных марок стали, коэффициент Пуассона изменяется в пределах 0,25 – 0,3. Для других материалов его значения приводятся в справочной литературе.
9.6. Перемещение поперечных сечений стержня
При нагружении стержня осевыми силами возникает деформирование, при котором произвольная точка его оси перемещается в другое положение. Величина этого перемещения равняется абсолютной деформации части стержня, расположенной между его закреплением и точкой, перемещение которой определяется.
Рис. 9.9
Рассмотрим прямой стержень, жестко закрепленный сверху и нагруженный внизу растягивающей силой F (рис. 9.9,а). Определим вертикальное перемещение точки b оси стержня.
Следует помнить, что все точки поперечного сечения стержня, проведенного через точку b,имеют одинаковые вертикальные перемещения. То есть, определяя перемещение точек оси стержня, мы определяем перемещение поперечных сечений этого стержня.
Проведем через точку b поперечное сечение 1-1 и отбросим условно нижнюю часть. В сечении 1-1 верхней части приложим продольную силу N = F (рис. 9,9,б), тогда вертикальное перемещение точки b будет равняться абсолютной продольной деформации верхней части стержня. Используем формулу (9.10) для одного участка стержня и получим величину вертикального перемещения точки b.
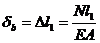(9.15)
Если стержень имеет несколько участков между закреплением и точкой, в которой определяется перемещение, то нужно применить общую формулу (9.11).
