Рис. 7.4
Рассмотрим правую отсеченную часть бруса, представленного на рис.7.3. Выберем произвольную точку сечения с положительными координатами и наметим вокруг этой точки элементарную площадку 
(рис.7.4). На эту площадку будет действовать некоторая элементарная внутренняя сила 
. Напомним, что внутренние силы, которые возникают в произвольном сечении бруса, распределены по всей площади этого сечения. Составляющие внутренних сил, которые являются сосредоточенными силами и моментами, нужно рассматривать как статический эквивалент распределенных нагрузок.
Интенсивность распределенных внутренних сил в произвольной точке сечения называется напряжением. Напряжение в точке может быть средним и полным.
Среднее напряжение pср равняется отношению элементарной величины внутренней силы , которая действует на элементарную часть площади сечения, к величине этой части площади (рис.7.4), то есть:
(7.2)
Полное напряжение p в точке сечения равняется пределу среднего напряжения, когда величина элементарной площади стремится к нулю, т.е.:
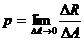(7.3)
Рис. 7.5
Напряжение является векторной величиной и в общем случае не является перпендикулярным к плоскости сечения и не расположено в этой плоскости. Оно действует под некоторым углом относительно плоскости сечения, или относительно нормали к этой плоскости (рис.7.5). При этом линии действия среднего и полного напряжений в общем случае не совпадают.
Разложим полное напряжение p на две составляющие – нормальную и касательную. Нормальная составляющая полного напряжения действует в направлении нормали к плоскости сечения и называется нормальным напряжением σ в точке сечения. Касательная составляющая действует в плоскости сечения и называется касательным напряжением 
. Поскольку эти напряжения взаимно перпендикулярны, то их равнодействующая p будет определяться по известной формуле:
(7.4)
В общем случае касательное напряжение не является параллельным главным осям y и z поперечного сечения, поэтому оно может быть разложено на две составляющие параллельные этим осям, т. е. составляющие 
и 
, при этом:
(7.5)
Нормальные и касательные напряжения в сопротивлении материалов играют очень важную роль, потому что от них зависит прочность элементов машин и инженерных сооружений. Эти напряжения связаны с внутренними усилиями и определяются в зависимости от вида деформации бруса. В следующих главах будут выведены основные формулы для определения нормальных и касательных напряжений.
