При построение доверительного интервала для индивидуальных значений результативного признака 
, в отличие от доверительного интервала для функции регрессии необходимо учитывать вариацию вокруг линии регрессии. В результате стандартная ошибка индивидуальных значений 
при 
равна
(9.106)
Доверительный интервал примет вид:
(9.107)
где
- предельная ошибка
(9.108)
Точность интервала рассчитывают как отношение максимального значения интервала к минимальному значению
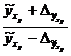(9.109)
Чем меньше отношение, тем меньше интервал, то есть он более точен.
Расчет доверительных интервалов для параметров уравнения регрессии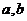 
Для свободного члена уравнения регрессии 
доверительный интервал имеет вид:
(9.110)
Где
- предельная ошибка
(9.111)
- стандартная ошибка
(9.112)
Для коэффициента регрессии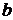 
доверительный интервал имеет вид:
(9.113)
где
- предельная ошибка
(9.114)
- стандартная ошибка
(9.115)
Пример 9.20. По данным примера 9.7 и примера 9.9, необходимо:
1. провести прогнозирование на основе парной линейной модели регрессии 
для индивидуального значения результативного признака при 
.
2. рассчитать доверительные интервалы для
а) функции регрессии
б) индивидуального прогнозного значения , при
в) свободно члена уравнения регрессии 
г) коэффициента регрессии 
Решение.
1) Рассчитаем прогнозное значение результативного признака, подставив индивидуальное значение фактора 
в линейное уравнение регрессии
2) Рассчитаем доверительные интервалы
a) Доверительный интервал прогноза для функции регрессии рассчитаем как:
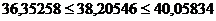
Где:
Для расчетов используем таблицу 9.34.
табличное значение критерия Стьюдента для числа степеней свободы 
и определенного уровня значимости 
.
Доверительный интервал прогноза показывает, что с вероятностью 
прогнозное значение 
средней прибыли по совокупности предприятий для конкретного значения фактора 
будет находиться в интервале от 36,35258 до 40,05834, не принимая нулевых значений, т.е. являются статистически значимыми.
Таблица 9.34
| № | 
| 
| 
| 
| 
| 
|
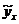
| 1 | 37,80 | 0,30 | 0,09 | 37,792344 | 1,886044 | 0,000059 |
| 2 | 38,00 | 0,50 | 0,25 | 38,028410 | 1,376710 | 0,000807 |
| 3 | 39,00 | 0,70 | 0,49 | 38,264476 | 0,947377 | 0,540996 |
| 4 | 37,50 | 0,80 | 0,64 | 38,382510 | 0,762711 | 0,778824 |
| 5 | 39,50 | 0,90 | 0,81 | 38,500543 | 0,598044 | 0,998914 |
| 6 | 36,80 | 1,10 | 1,21 | 38,736609 | 0,328711 | 3,750454 |
| 7 | 40,00 | 1,30 | 1,69 | 38,972676 | 0,139378 | 1,055395 |
| 8 | 40,10 | 1,60 | 2,56 | 39,326775 | 0,005378 | 0,597877 |
| 9 | 40,00 | 1,70 | 2,89 | 39,444808 | 0,000711 | 0,308238 |
| 10 | 39,00 | 2,20 | 4,84 | 40,034974 | 0,277378 | 1,071171 |
| 11 | 38,00 | 2,50 | 6,25 | 40,389074 | 0,683378 | 5,707675 |
| 12 | 41,00 | 2,60 | 6,76 | 40,507107 | 0,858712 | 0,242944 |
| 13 | 41,60 | 2,70 | 7,29 | 40,625140 | 1,054045 | 0,950352 |
| 14 | 41,00 | 3,00 | 9,00 | 40,979240 | 1,760045 | 0,000431 |
| 15 | 41,90 | 3,20 | 10,24 | 41,215306 | 2,330712 | 0,468806 |
| Итого | 591,20 | 25,10 | 55,01 | 591,199992 | 13,009333 | 16,472942 |
| В среднем | 1,673333 |
б) Рассчитаем доверительный интервал для индивидуального прогнозного значения , при
Доверительный интервал примет вид:
Доверительный интервал прогноза показывает, что с вероятностью прогнозное значение 
индивидуальной средней прибыли для конкретного значения фактора 
будет находиться в интервале от 35,148114 до 41,262806, не принимая нулевых значений, т.е. являются статистически значимыми.
в) Рассчитаем доверительный интервал для свободного члена уравнения 
.
где
Доверительный интервал прогноза показывает, что с вероятностью значение параметра 
находится в интервале от 36,147123 до 38,729365, не принимая нулевых значений, т.е. являются статистически значимыми.
г) Для коэффициента регрессии доверительный интервал имеет вид:
где
Доверительный интервал показывает, что с вероятностью прогнозное значение 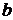будет находиться в интервале от 0,505907 до 0,674425, не принимая нулевых значений, т.е. является статистически значимым.
