Коэффициенты регрессии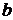 
выражены в натуральных единицах, то есть являются именованными величинами, поэтому коэффициенты регрессии, выраженные в разных единицах несопоставимы между собой. Для сопоставления разноименных коэффициентов корреляции линейных и нелинейных моделей удобно использовать коэффициент эластичности.
(9.76)
где:
- первая производная функции регрессии для соответствующей формы связи.
Так как коэффициент эластичности не всегда величина постоянная, а часто зависит от значения 
, обычно рассчитывают средний коэффициент эластичности.
(9.77)
Коэффициент средней эластичности для некоторых функций рассчитывается как:
· уравнение прямой 
:
(9.78)
· парабола второго порядка 
· уравнение равносторонней гиперболы 
:
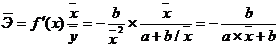(9.79)
· степенного уравнения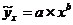 
:
(9.80)
· показательного уравнения 
:
(9.81)
Коэффициент средней эластичности показывает, на сколько процентов в среднем изменится результативный признак, если факторный признак увеличится на один процент.
Коэффициент средней эластичности позволяет ранжировать факторы по силе влияния на результат, чем больше коэффициент для 
-го фактора, тем сильнее данный фактор влияет на результат.
Пример 9.15. Исходя из рассчитанных уравнений регрессии (табл. 9.30) рассчитать коэффициенты средней эластичности для линейной функции, полинома второй степени, равносторонней гиперболы, степенной и показательной функций.
Таблица 9.30
| Функция | Уравнение регрессии | 
|
| Линейная | 
|
1,6713 |
| Парабола второй степени |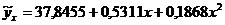 
| |
| Равносторонняя гипербола |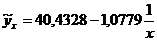 
| |
| Степенная | 
| |
| Показательная | 
|
Рассчитать коэффициенты средней эластичности для каждого уравнения регрессии.
Решение.
1. Для линейной функции
2. Для полинома второй степени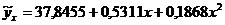
3. Для равносторонней гиперболы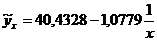
4. Для степенной функции
5. Для показательной функции
Пример 9.16. По группе предприятий, рассчитаны уравнения парной линейной регрессии, отражающие зависимость средней прибыли от уровня оплаты труда и затрат на маркетинг (табл. 9.31).
Таблица 9.31
| Признак-фактор | Уравнение парной линейной регрессии | Среднее значение фактора
|
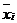
Уровень оплаты труда, 
| 
| 62,4 |
Затраты на маркетинг, 
| 
| 189,07 |
Используя коэффициенты средней эластичности определить степень влияния каждого из факторов.
Решение.
По формуле коэффициента средней эластичности для линейной функции рассчитаем данный коэффициент по каждому из факторов.
а) по фактору
б) по фактору 
Исходя из рассчитанных коэффициентов средней эластичности, можно сказать, что фактор оказывает более сильное влияние на урожайность, чем фактор .
