Простейшим методом определения наличия и формы взаимосвязи является построения корреляционной таблицы и графика «корреляционное поле».
Корреляционная таблица – таблица, в которой записываются частоты сочетаний результативного и факторного показателей. В настоящее время корреляционная таблица не используется для вычисления уравнения связи.
Пример 9.8. Имеются данные о себестоимости единицы продукции 
(руб.) и затратах на рекламу 
(млн. руб.) (табл. 9.18).
Таблица 9.18
| 210 | 210 | 220 | 200 | 240 | 200 | 210 | 220 | 210 | 220 | 240 | 200 |
| 30 | 50 | 50 | 40 | 70 | 30 | 40 | 70 | 30 | 60 | 60 | 30 |
Составим корреляционную таблицу (табл. 9.19).
Таблица 9.19
| y x | 200 | 210 | 220 | 240 | Итого |
| 30 | 2 | 2 | 4 | ||
| 240 | 1 | 1 | 2 | ||
| 50 | 1 | 1 | 2 | ||
| 60 | 1 | 1 | 2 | ||
| 70 | 1 | 1 | 2 | ||
| Итого | 3 | 4 | 3 | 2 | 12 |
По корреляционной таблице можно сделать следующие выводы. Если и распложены по возрастанию, то расположение частот около диагонали таблицы слева вниз направо говорит о прямой форме связи, если по диагонали вверх направо, то связь обратная. Если частоты находятся равномерно по всей таблицы – связь слабая.
Корреляционное поле (графический метод изучения взаимосвязей) – точечный график, характеризующий единицу наблюдения по двум признакам. Факторный признак откладывается по оси абсцисс, результативный признак по оси ординат.
По данным примера 8 построим корреляционное поле (рис. 9.4).
Рисунок 9.4
Анализ корреляционного поля показывает, что имеется прямая связь.
Если связь между признаками обратная, то корреляционное поле будет иметь примерно такой вид (рис. 9.5).
Рисунок 9.5
Если корреляционное поле имеет следующий вид (рис. 6) можно сделать вывод об отсутствии выраженной взаимосвязи.
Рисунок 9.6
Корреляционная таблица и корреляционное поле показывают лишь наличие, отсутствие и направление связи. Но они не дают представления о тесноте, интенсивности связи между признаками.
Тесноту связи в парной линейной модели определяют, рассчитывая линейный коэффициент парной корреляции 
или просто коэффициент корреляции. Существуют формулы расчета:
(9.29)
или 
(9.30)
где: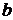 
- коэффициент регрессии;
- среднее квадратическое значение факторного признака;
- среднее квадратическое значение результативного признака;
(9.31)
где 
- сумма квадратов отклонений обусловленная влиянием фактора ;
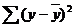- общая сумма квадратов отклонений признака .
Коэффициент корреляции также можно рассчитать через значение признаков в стандартизованном масштабе:
(9.32)
где: 
– значения признаков в стандартизованном масштабе.
(9.33)
(9.34)
Коэффициент корреляции может принимать значения от 
до 
. В статистике говорят, что если значения коэффициента парной корреляции:
· меньше 0,3 (-0,3) - связь положительная (отрицательная) слабая;
· от 0,3 до 0,7 (от -0,3 до -0,7) - связь положительная (отрицательная) средняя;
· свыше 0,7 (-0,7) - связь положительная (отрицательная) сильная;
· равен 1 (-1) - связь функциональная положительная (отрицательная);
· равен 0 – связь отсутствует.
Другой показатель тесноты связи – коэффициент парной детерминации. Он показывает часть вариации результативного признака, которая сложилась под влиянием включенного в парную модель фактора. Коэффициент парной детерминации 
рассчитывают, возводя в квадрат коэффициент парной корреляции 
или по формуле:
(9.35)
Коэффициент парной детерминации позволяет определять тесноту связи не только в линейных, но и в нелинейных моделях.
Коэффициент парной детерминации может принимать значения от 
до .
Пример 9.9. Имеются данные о средней прибыли (млн. руб.) и затратах на рекламу (млн. руб.) за декаду, по выборке, равной 15-ти предприятий сферы торговли (табл. 9.20).
Таблица 9.20
| № | 
| 
|
| 1 | 37,80 | 0,30 |
| 2 | 38,00 | 0,50 |
| 3 | 39,00 | 0,70 |
| 4 | 37,50 | 0,80 |
| 5 | 39,50 | 0,90 |
| 6 | 36,80 | 1,10 |
| 7 | 40,00 | 1,30 |
| 8 | 40,10 | 1,60 |
| 9 | 40,00 | 1,70 |
| 10 | 39,00 | 2,20 |
| 11 | 38,00 | 2,50 |
| 12 | 41,00 | 2,60 |
| 13 | 41,60 | 2,70 |
| 14 | 41,00 | 3,00 |
| 15 | 41,90 | 3,20 |
| Сумма | 591,20 | 25,10 |
| В среднем | 39,413333 | 1,673333 |
| 1,518713 | 0,931283 |
Рассчитать коэффициент парной линейной корреляции и коэффициент парной линейной регрессии .
Решение.
1) Так, как из примера 7 известно, что уравнение регрессии 
используем формулу:
Коэффициент парной корреляции 
показывает, что между исследуемыми признаками существует тесная положительная связь.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации.
Коэффициент детерминации показывает, что 52% от всей вариации результативного признака обусловлено влиянием включенного в модель фактора, а 48% вариации вызвано влиянием всех остальных, не исследуемых в данной модели факторами.
2) Рассмотрим решение данной задачи в Microsoft Excel.
В новой книге Microsoft Excel внесем исходные данные (рис 7).
Далее нажимаем кнопку Сервис и в открывшийся панели нажимаем кнопку Анализ данных
В панели Анализ данных нажимаем корреляция:
В панели корреляция вводим входной интервал, выделяя все столбики, содержащий и данные результативного признака и данные фактора. Ответ можно поместить на новом рабочем листе, в новой рабочей книге, или на листе, содержащем условия выбирая выходной интервал, для чего указываем графа-клетку начала размещения ответа (рис. 9.7).
Рисунок 9.7
Нажимаем ОК.
Появится таблица парных линейных коэффициентов корреляции (рис. 9.8).
Рисунок 9.8
На пересечении столбца 1 и столбца 2 и будет искомый коэффициент парной линейной корреляции.
