Как и в парной линейной регрессии, в регрессии нелинейной оценку надежности уравнения в целом проводят с помощью критерия Фишера (F-критерия), а оценку параметров уравнения и коэффициента детерминации проводят с помощью критерия Стьюдента.
Общая формула фактического F-критерия имеет вид;
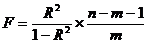 (9.85)
(9.85)
где:
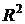 - индекс детерминации.
- индекс детерминации.
 - число наблюдений.
- число наблюдений.
 - число параметров при переменных
- число параметров при переменных  .
.
В случае нелинейной регрессии  отлично для разных видов регрессии, и формула F-критерия различна для различных функций.
отлично для разных видов регрессии, и формула F-критерия различна для различных функций.
Например. Для степенной  и показательной
и показательной 
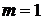 и:
и:
 (9.86)
(9.86)
Для параболы второго порядка 
 и:
и:
 (9.87)
(9.87)
Для параболы третьего порядка 
 и:
и:
 (9.88)
(9.88)
Как и в случае линейной регрессии, критерий Фишера фактический сравнивают с критерием Фишера табличным, при определенном уровне значимости  или
или  , и числе степеней свободы -
, и числе степеней свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2).
(таблицы Снедекора-Фишера – приложение 2).
Значимость параметров уравнения парной нелинейной регрессии и индекса корреляции проверяется, аналогично парной линейной регрессии, используя критерий Стьюдента.
Критерий Стьюдента для коэффициента регрессии 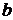 рассчитывается как;
рассчитывается как;
 (9.89)
(9.89)
где; 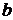 - коэффициент регрессии.
- коэффициент регрессии.
 - стандартная ошибка коэффициента регрессии, рассчитывается как:
- стандартная ошибка коэффициента регрессии, рассчитывается как:
 (9.90)
(9.90)
Учитывая, что 
 (9.91)
(9.91)
Критерий Стьюдента для параметра  рассчитывается как;
рассчитывается как;
 (9.92)
(9.92)
где:  - свободный член уравнения регрессии.
- свободный член уравнения регрессии.
 - стандартная ошибка параметра
- стандартная ошибка параметра  , рассчитывается как:
, рассчитывается как:
 (9.93)
(9.93)
или  (9.94)
(9.94)
Критерий Стьюдента для индекса корреляции  рассчитывается как;
рассчитывается как;
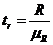 (9.95)
(9.95)
или  (9.96)
(9.96)
где:  - индекс корреляции.
- индекс корреляции.
 - стандартная ошибка индекса корреляции, рассчитывается как:
- стандартная ошибка индекса корреляции, рассчитывается как:
 (9.97)
(9.97)
Качество подбора модели  определяют, рассчитывая среднюю ошибку аппроксимации. Для расчета средней ошибки аппроксимации используют формулы:
определяют, рассчитывая среднюю ошибку аппроксимации. Для расчета средней ошибки аппроксимации используют формулы:
 (9.98)
(9.98)
 (9.99)
(9.99)
где  (9.100)
(9.100)
 (9.101)
(9.101)
Чем меньше средняя ошибка аппроксимации, тем выше качество модели. Допустимый предел 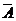 не более 10%.
не более 10%.
Пример 9.18. Необходимо оценить существенность уравнения регрессии равносторонней гиперболы  , при:
, при:
где:  - индекс детерминации.
- индекс детерминации.
 - число наблюдений.
- число наблюдений.
Решение. Оценку существенности уравнения нелинейной регрессии проведем, используя критерий Фишера (F-критерий)
 .
.
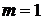 - число параметров при переменных
- число параметров при переменных  .
.
Найдем критерий Фишера табличный, при уровне значимости  , и числе степеней свободы -
, и числе степеней свободы -  ,
,  (таблицы Снедекора-Фишера – приложение 2) -
(таблицы Снедекора-Фишера – приложение 2) -  .
.
Так как  уравнение регрессии признаем статистически значимым.
уравнение регрессии признаем статистически значимым.
Пример 9.19. По данным примеров 9.7; 9.11; 9.12; 9.13; 9.14 рассчитаем средние ошибки аппроксимации для линейной функции, функции параболы второй степени, равносторонней гиперболы, степенной и показательной функций.
Решение. Для расчета средней ошибки аппроксимации используем формулу:
 , где
, где 
Расчет произведем в таблице 9.33. Средние ошибки аппроксимации составили для:
· линейной функции 
· параболы второго порядка 
· функции равносторонней гиперболы 
· степенной функции 
· показательной функции 
Соответственно линейная функция наиболее качественно описывает существующую взаимосвязь между исследуемыми явлениями. Но все регрессии находятся в допустимых пределах ( не более 10%).
не более 10%).
Таблица 9.33
|
№ |
| Линейная
| Парабола второго порядка
| Гипербола
| ||||||

| 
| 
| 
| 
| 
| 
| 
| 
| ||
| 1 | 37,8 | 37,792344 | 0,007656 | 0,020254 | 38,023560 | 0,223560 | 0,591429 | 36,808395 | 0,991605 | 2,623294 |
| 2 | 38,0 | 38,028410 | 0,028410 | 0,074763 | 38,158005 | 0,158005 | 0,415803 | 38,266516 | 0,266516 | 0,701358 |
| 3 | 39,0 | 38,264476 | 0,735524 | 1,885959 | 38,307508 | 0,692492 | 1,775621 | 38,891425 | 0,108575 | 0,278397 |
| 4 | 37,5 | 38,382510 | 0,882510 | 2,353360 | 38,387907 | 0,887907 | 2,367752 | 39,086709 | 1,586709 | 4,231224 |
| 5 | 39,5 | 38,500543 | 0,999457 | 2,530271 | 38,472071 | 1,027929 | 2,602352 | 39,238597 | 0,261403 | 0,661780 |
| 6 | 36,8 | 38,736609 | 1,936609 | 5,262524 | 38,651694 | 1,851694 | 5,031777 | 39,459524 | 2,659524 | 7,226967 |
| 7 | 40,0 | 38,972676 | 1,027324 | 2,568310 | 38,846375 | 1,153625 | 2,884063 | 39,612474 | 0,387526 | 0,968815 |
| 8 | 40,1 | 39,326775 | 0,773225 | 1,928242 | 39,166634 | 0,933366 | 2,327596 | 39,770204 | 0,329796 | 0,822434 |
| 9 | 40,0 | 39,444808 | 0,555192 | 1,387980 | 39,280917 | 0,719083 | 1,797708 | 39,810409 | 0,189591 | 0,473978 |
| 10 | 39,0 | 40,034974 | 1,034974 | 2,653779 | 39,908803 | 0,908803 | 2,330264 | 39,956611 | 0,956611 | 2,452849 |
| 11 | 38,0 | 40,389074 | 2,389074 | 6,287037 | 40,330713 | 2,330713 | 6,133455 | 40,016262 | 2,016262 | 5,305953 |
| 12 | 41,0 | 40,507107 | 0,492893 | 1,202178 | 40,478879 | 0,521121 | 1,271027 | 40,033086 | 0,966914 | 2,358327 |
| 13 | 41,6 | 40,625140 | 0,974860 | 2,343413 | 40,630810 | 0,969190 | 2,329784 | 40,048664 | 1,551336 | 3,729173 |
| 14 | 41,0 | 40,979240 | 0,020760 | 0,050634 | 41,109192 | 0,109192 | 0,266322 | 40,089168 | 0,910832 | 2,221541 |
| 15 | 41,9 | 41,215306 | 0,684694 | 1,634115 | 41,446938 | 0,453062 | 1,081294 | 40,111951 | 1,788049 | 4,267420 |
| Итого | 591,2 | 32,182820 | 33,206244 | 38,323509 | ||||||
| В среднем |
|
|
| 2,145521 |
|
| 2,213750 |
|
| 2,554901 |
Продолжение табл. 9.33
|
№ |
| Степенная
| Показательная
| ||||

| 
| 
| 
| 
| 
| ||
| 1 | 37,8 | 37,183851 | 0,616149 | 1,630024 | 37,806262 | 0,006262 | 0,016566 |
| 2 | 38,0 | 37,910774 | 0,089226 | 0,234805 | 38,032035 | 0,032035 | 0,084303 |
| 3 | 39,0 | 38,397333 | 0,602667 | 1,545300 | 38,259157 | 0,740843 | 1,899597 |
| 4 | 37,5 | 38,592153 | 1,092153 | 2,912408 | 38,373226 | 0,873226 | 2,328603 |
| 5 | 39,5 | 38,764817 | 0,735183 | 1,861223 | 38,487635 | 1,012365 | 2,562949 |
| 6 | 36,8 | 39,060772 | 2,260772 | 6,143402 | 38,717477 | 1,917477 | 5,210535 |
| 7 | 40,0 | 39,308870 | 0,691130 | 1,727825 | 38,948692 | 1,051308 | 2,628270 |
| 8 | 40,1 | 39,619441 | 0,480559 | 1,198401 | 39,298106 | 0,801894 | 1,999736 |
| 9 | 40,0 | 39,710581 | 0,289419 | 0,723548 | 39,415272 | 0,584728 | 1,461820 |
| 10 | 39,0 | 40,100534 | 1,100534 | 2,821882 | 40,006365 | 1,006365 | 2,580423 |
| 11 | 38,0 | 40,295293 | 2,295293 | 6,040245 | 40,365268 | 2,365268 | 6,224389 |
| 12 | 41,0 | 40,355237 | 0,644763 | 1,572593 | 40,485616 | 0,514384 | 1,254595 |
| 13 | 41,6 | 40,413002 | 1,186998 | 2,853361 | 40,606323 | 0,993677 | 2,388647 |
| 14 | 41,0 | 40,574705 | 0,425295 | 1,037305 | 40,970608 | 0,029392 | 0,071688 |
| 15 | 41,9 | 40,674075 | 1,225925 | 2,925835 | 41,215278 | 0,684722 | 1,634181 |
| Итого | 591,2 | 35,228156 | 590,987320 | 32,346303 | |||
| В среднем |
|
| 2,348544 |
|
| 2,156420 | |










