Оценка надежности уравнения парной линейной регрессии, его параметров и коэффициента парной линейной корреляции

Результаты корреляционно-регрессионного анализа необходимо проверить, проведя оценку существенности, как уравнения регрессии, так и его параметров и коэффициента корреляции.

Оценка существенности уравнения регрессии в целом проводится с помощью критерия Фишера – F-критерия.

При этом исходят из представления, что если между изучаемыми признаками  и  есть связь и уравнение парной линейной регрессии эту связь отражает, то вариация результативного признака , обусловленная влиянием факторного признака  (факторная вариация) должна быть в несколько раз больше, чем вариация результативного признака, вызванная всеми другими факторами (остаточная вариация).

Для этого вначале проводят исследование дисперсии.

Общую сумму квадратов отклонений раскладывают на две части – «факторную» и «остаточную».

                                                                     (9.36)

где: - общая сумма квадратов отклонений;

- факторная сумма квадратов отклонений;

- остаточная сумма квадратов отклонений.

Разделив каждую сумму квадратов отклонений на соответствующее число степеней свободы (  для общей суммы,  для факторной и  для остаточной) получим дисперсию на одну степень свободы - .

                                                                                                    (9.37)

                                                                                             (9.38)

                                                                                            (9.39)

Для расчета F-критерия сопоставим факторную и остаточную дисперсию;

                                                                                                             (9.40)

Также F-критерий можно рассчитать по формуле:

                                                                                                        (9.41)

Оценку существенности уравнения регрессии проводят, сравнивая полученное значение F-критерия () с табличным значением (), которое берут из таблиц критических значений F-отношений при определенном уровне значимости, как правило:  или , и числе свободы: ,  (таблицы Снедекора-Фишера – приложение 2).

Если  то уравнение регрессии значимо, если меньше незначимо.

Значимость параметров уравнения  и коэффициента корреляции  проверяют при помощи критерия Стьюдента – t-критерия.

Критерий Стьюдента для коэффициента регрессии 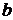 рассчитывается как;

                                                                                                                         (9.42)

где; 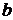- коэффициент регрессии.

 - стандартная ошибка коэффициента регрессии, рассчитывается как:

                                                                                         (9.43)

Учитывая, что

                                                                                                        (9.44)

Критерий Стьюдента для параметра  рассчитывается как;

                                                                                                                         (9.45)

где: - свободный член уравнения регрессии.

 - стандартная ошибка параметра , рассчитывается как:

                                                                           (9.46)

или                                                                                      (9.47)

Критерий Стьюдента для коэффициента корреляции  рассчитывается как;

                                                                                                                         (9.48)

или                                                                                          (9.49)

где:  - коэффициент парной линейной корреляции.

- стандартная ошибка коэффициента корреляции, рассчитывается как:

                                                                                                                (9.50)

Кроме того, для парной линейной регрессии верно, что:

                                                                                                                (9.51)

Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости ,  или , и числе степеней свободы  (приложение 1), где - число единиц наблюдения, - число параметров уравнения регрессии. Если фактическое значение  больше табличного соответствующий коэффициент статистически значим.

 

Пример 9.10. По данным примера 7 и примера 9 провести оценку существенности полученного уравнения регрессии , его параметров ,  и коэффициента корреляции . 

Решение.

1. Оценка статистической значимости функции регрессии проводится при помощи критерия Фишера – F-критерия.

Рассчитаем для парной линейной регрессии . Расчет  проведем по формуле:

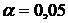Далее фактическое значение  необходимо сравнить с табличным значением. Табличное значение берется из таблиц значения  Фишера при разных уровнях значимости  (приложение 2). При  и числе степеней свободы , , . Так как 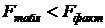, можно сказать, что уравнение регрессии статистически значимо.

2. Оценка статистической значимости параметров уравнения регрессии  и коэффициента парной линейной корреляции  проводится при помощи критерия Стьюдента – t-критерия.

Для расчета критерия Стьюдента составим таблицу 9.21.

Таблица 9.21

№
1	37,80	0,30	0,09	37,792344	0,000059	1,886044
2	38,00	0,50	0,25	38,028410	0,000807	1,376710
3	39,00	0,70	0,49	38,264476	0,540996	0,947377
4	37,50	0,80	0,64	38,382510	0,778824	0,762711
5	39,50	0,90	0,81	38,500543	0,998914	0,598044
6	36,80	1,10	1,21	38,736609	3,750454	0,328711
7	40,00	1,30	1,69	38,972676	1,055395	0,139378
8	40,10	1,60	2,56	39,326775	0,597877	0,005378
9	40,00	1,70	2,89	39,444808	0,308238	0,000711
10	39,00	2,20	4,84	40,034974	1,071171	0,277378
11	38,00	2,50	6,25	40,389074	5,707675	0,683378
12	41,00	2,60	6,76	40,507107	0,242944	0,858712
13	41,60	2,70	7,29	40,625140	0,950352	1,054045
14	41,00	3,00	9,00	40,979240	0,000431	1,760045
15	41,90	3,20	10,24	41,215306	0,468806	2,330712
Сумма	591,20	25,10	55,01	591,199992	16,472942	13,009333
В среднем		1,673333

 

Фактически критерий Стьюдента для коэффициента регрессии  рассчитывается как;

.

Значение стандартных ошибок , можно взять из результатов регрессионного анализа в Microsoft Excel – рисунок 3, столбец – стандартная ошибка.

Фактический критерий Стьюдента для свободного члена уравнение регрессии  рассчитывается как:

.

.

Фактически критерий Стьюдента для коэффициента корреляции  рассчитывается как;

Также верно, что  

Полученные фактические критерии Стьюдента с табличным значением (приложение 1) при определенном уровне значимости и числе степеней свободы . Если фактические значения t-критерия превышают табличные можно принять, что соответствующее расчетное значение статистически значимо.

Для данного примера табличное значение, при  и составит . Все фактические значения t-критерия превышают табличные. Можно сделать вывод о статистической значимости параметров уравнения регрессии  и коэффициента парной линейной корреляции  для парной линейной регрессии выраженной уравнением .

2) Расчет фактического критерия Фишера и критерия Стьюдента в Microsoft Excel.

Фактические значения критериев Фишера и Стьюдента представлены в итоговой таблице, содержащей результаты регрессионного анализа – пример 7, рис. 3.

Критерий Фишера расчетный обозначен в столбике F дисперсионного анализа, t-критерии для параметров уравнения   в столбике t-статистика.